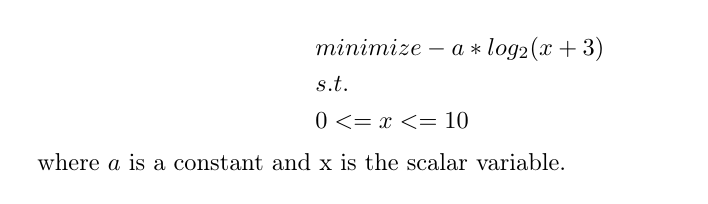For the convex optimization problem below, I got a “unbounded” result by cvx toolbox. I don’t know the specific reason behind the phenomenon, and how to avoid similar problem in the future? So ask for help. Thanks!
Set the constant parameter a as 10^9.
The code:

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:34:40)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86
MOSEK warning 52: A numerically large lower bound value -1.4e+09 is specified for constraint ‘’ (1).
MOSEK warning 53: A numerically large upper bound value -1.4e+09 is specified for constraint ‘’ (1).
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 2
Cones : 1
Scalar variables : 6
Matrix variables : 0
Integer variables : 0
Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 2 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.01
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 2
Cones : 1
Scalar variables : 6
Matrix variables : 0
Integer variables : 0
Optimizer - threads : 4
Optimizer - solved problem : the primal
Optimizer - Constraints : 1
Optimizer - Cones : 1
Optimizer - Scalar variables : 5 conic : 3
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 1 after factor : 1
Factor - dense dim. : 0 flops : 9.00e+00
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 1.4e+09 1.0e+01 1.2e+09 0.00e+00 2.252555693e+00 -1.161516665e+09 1.0e+00 0.03
1 8.4e+06 5.8e-02 8.9e+07 -1.00e+00 2.534263193e+03 -1.161579996e+09 5.8e-03 0.06
2 1.3e+02 8.9e-07 3.5e+05 -1.00e+00 1.658827461e+08 -9.776015838e+08 8.9e-08 0.06
3 1.3e+01 8.8e-08 1.0e+05 -9.87e-01 1.534024793e+09 5.524652195e+08 8.8e-09 0.06
Optimizer terminated. Time: 0.09
Interior-point solution summary
Problem status : PRIMAL_INFEASIBLE
Solution status : PRIMAL_INFEASIBLE_CER
Dual. obj: 5.1941585114e+00 nrm: 1e-08 Viol. con: 0e+00 var: 8e-09 cones: 0e+00
Optimizer summary
Optimizer - time: 0.09
Interior-point - iterations : 3 time: 0.08
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
Status: Unbounded
Optimal value (cvx_optval): -Inf
It is not surprising, you are trying to solve a problem where the expected objective value is of order 10^{10}. That is wishful thinking. Keep your model more numerically sane, so that everything is roughly on similar scale and that you don’t have such explosions. See for example 7 Practical optimization — MOSEK Modeling Cookbook 3.3.0
OK. Thank you! I will refer to this literature.