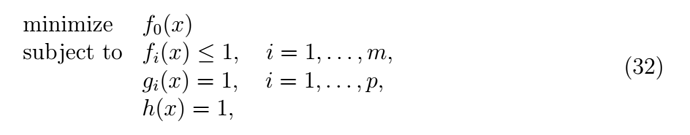The Generalized Geometric Programming (GPP) can be defined as
My question:
Since
\bar{x}=\{\bar{x}_1,\cdots,\bar{x}_k,\cdots,\bar{x}_n\} is the global optimal solution of (33), why the increasing of
\bar{x}_k still can continue decrease the objective function in (33) and satisfies the constraints in (33). I think it doesn’t make sense because if
\bar{x}^{\dag}=\{\bar{x}_1,\cdots,\bar{x}_k+u,\cdots,\bar{x}_n\} (
u>0) is the modified solution to (33) and can lead to a more smaller optimal value, then
\bar{x}^{\dag} is a new optimal solution to (33). Why the GPP (33) gives a suboptimal solution
\bar{x} when we solve it at beginning. (Note that (33) can be converted into a convex problem which means that when (33) is solved, the solution is just the optimal and no need any modification.)
I think that increasing \bar{x}_k cannot further decrease objective function, but may be only lead to the objective function remain constant.
However, I do believe Prof. Boyd definitely do not make fault on this!
Is anyone can give me some instruction for my above question? Many thanks.
I think you are misinterpreting what is meant by “… has an objective value that is the same, or better than, the point …” . Because the objective value can not get better than the global optimum solution, it therefore stays the same. Once h(x) = 1 is obtained, there is now a solution of the relaxation which satisfies the constraints to the original problem, and therefore is globally optimal for it. This new point is an alternative globally optimal point to the relaxation, but unlike the originally globally optimal solution to the relaxation which was not feasible for the original problem, this one is.
I think you are interpreting the statement as a layman, whereas it is written as a math statement. Just because x <= y., it doesn’t necessarily mean that x has any chance of being less than y.
Thanks four your critical reply! [quote=“Mark_L_Stone, post:2, topic:3671”]
Because the objective value can not get better than the global optimum solution, it therefore stays the same.
[/quote]
Does that mean the new point actually cannot make a better optimal value but only keep the objective value same?
Yes, I believe that to true.
Thank you, Mark L. Stone!
Another question: If every x_k can not keep the objective value unchanging but only increasing the value. Does that mean I can only obtain a sub-optimal solution to the original problem if I still adjust the obtained optimal solution to the relaxed problem.
You would have no guarantee of optimality for the original problem… However, it might be optimal. It might not.
OK, I got it. Thank you, Mark!