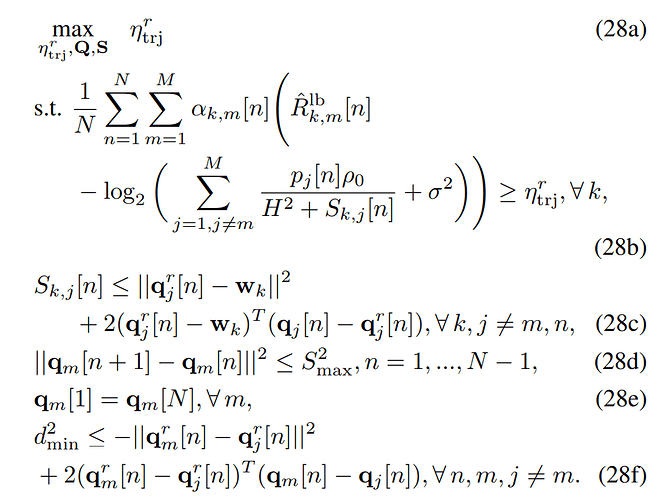Hello everyone! I try to reproduce a paper which is about UAV trajectory optimization. My code is as follows. But when I run my code, I always get infeasible result. I don’t know how to solve it. Can you help me?
Here my mathematical formulas and code
Blockquote
clc;
d_min = 100;
P_max = 0.1;
v_max = 50;
noise_power = -110;
K = 6;
M = 2;
T = 100;
N = 200;
noise=10.^((noise_power-30)/10);
H = 100;
rho = 10^(-6);a1=zeros(K,N);
a2=zeros(K,N);
a1(1,:)=ones(1,N)(1/3);
a1(2,:)=ones(1,N)(1/3);
a1(3,:)=ones(1,N)(1/3);
a2(4,:)=ones(1,N)(1/3);
a2(5,:)=ones(1,N)(1/3);
a2(6,:)=ones(1,N)(1/3);p1=ones(K,N)*P_max;
p2=ones(K,N)*P_max;x1=[-1200,-700,-400,200,800,600];
y1=[600,-600,400,200,-400,1100];
z1=zeros(1,K);
plot(x1,y1,‘bo’);
hold on;
w=zeros(3,N,K);
for k=1:K
for n=1:N
w(:,n,k)=[x1(k),y1(k),z1(k)]';
end
end
q1_pre=zeros(3,N);
q2_pre=zeros(3,N);
c1=(w(:,1,1)+w(:,1,2)+w(:,1,3))/3;
c2=(w(:,1,4)+w(:,1,5)+w(:,1,6))/3;
ru1=max([norm(w(:,1,1)-c1),norm(w(:,1,2)-c1),norm(w(:,1,3)-c1)]);
ru2=max([norm(w(:,1,4)-c2),norm(w(:,1,5)-c2),norm(w(:,1,6)-c2)]);
r_max1=v_maxT/(2pi);
r_max2=v_maxT/(2pi);
r_trj1=min(ru1,r_max1);
r_trj2=min(ru2,r_max2);
for n=1:N
q1_pre(:,n)=[c1(1)+r_trj1cos(2pi*(n-1)/(N-1)),c1(2)+r_trj1sin(2pi*(n-1)/(N-1)),H];
q2_pre(:,n)=[c2(1)+r_trj2cos(2pi*(n-1)/(N-1)),c2(2)-r_trj2sin(2pi*(n-1)/(N-1)),H];
endd1=zeros(K,N);
d2=zeros(K,N);
for k=1:K
for n=1:N
d1(k,:)=norm(q1_pre(:,n)-w(:,n,k));
d2(k,:)=norm(q2_pre(:,n)-w(:,n,k));
end
endtemp=p1rho./d1.^2+p2rho./d2.^2;
I1=(p1rho./d1.^4)./(log(2)(temp+noise));
I2=(p2rho./d2.^4)./(log(2)(temp+noise));cvx_begin
cvx_solver Mosek
% cvx_quiet true
variable R_traj
variable q1(3,N)
variable q2(3,N)
variable S1(K,N)
variable S2(K,N)
expression R1_lb(K,N)
expression R2_lb(K,N)
expression t1(K,N)
expression t2(K,N)
expression r1(K,N)
expression r2(K,N)for k=1:K r1(k,:)=sum_square(q1-w(:,:,k)); r2(k,:)=sum_square(q2-w(:,:,k)); t1(k,:)=sum((q1_pre-w(:,:,k)).*(q1-q1_pre)); t2(k,:)=sum((q2_pre-w(:,:,k)).*(q2-q2_pre)); end R1_lb=-I1.*(r1-d1.^2)-I2.*(r2-d2.^2)+log2(temp+noise); R2_lb=R1_lb; maximize (R_traj) subject to (1/N)*sum(a1.*(R1_lb+log(1-inv_pos((S2./p2)+1))/log(2))+... a2.*(R2_lb+log(1-inv_pos((S1./p1)+1))/log(2)),2) >= R_traj; S1 <= d1.^2+2*t1; S2 <= d2.^2+2*t2; for n=1:N-1 sum_square(q1(:,n+1)-q1(:,n)) <= (v_max*T/N)^2; sum_square(q2(:,n+1)-q2(:,n)) <= (v_max*T/N)^2; end sum_square(q1_pre-q2_pre)+2*sum((q1_pre-q2_pre).*(q1-q2-q1_pre+q2_pre)) >= d_min^2; q1(:,1) == q1(:,N); q2(:,1) == q2(:,N); q1(3,:) == H; q2(3,:) == H;cvx_end