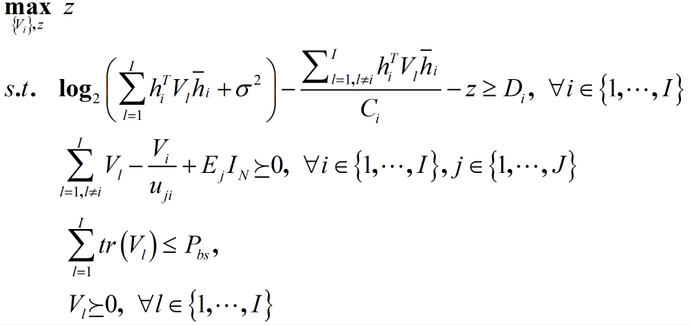I encounter the following convex problem:
In this problem, the variables needed to be optimized are V_i (i from 1 to I), which are a series of N*N hermitian semidefinite matrices and a scalar z.
P_{bs} is a given constant.
C_i, D_i and E_i are given constants (i from 1 to I).
u_{j,i} are also constants (i from 1 to I and j from 1 to J).
I_N is identity matrix.
h_i are given complex column vector (i from 1 to I).
Here is the code:
sumV_i in this code represent
\sum\limits_{l = 1,l \ne i}^I {{V_l}} and its dimension is
N*N*I .
The error occurs in second constraint,

I think the CVX misunderstand the >=, it does not mean “large than”, it actually means “the left hand side of the matrix is positive semidefinite matrix”. But i don’t know how to make CVX understand this operation.
I see. I have another question, if CVX work in SDP mode and i want to define a nonnegative matrix C>=0 (this >= means each element is no smaller than 0), will it treat this as a postive semidefinite constraint instead of element-wise nonnegative constraint?
Yes,. But you can use
vec(C) >= 0
or
C(:) >= 0
But of course, CVX doesn’t allow complex inequalities, so if C is complex, you can use
real(C(:)) >= 0
and/or
imag(C(:)) >= 0
depnending on what you want. Or use vec instead of (:) .
Or don’t use sdp mode and use one of the other options provided in the link to specify semdefinite constraints.
I have one last question. After i specify “variable V(N,N,I) complex semidefinite” in the code, do i need to explicitly add constraints
for i = 1:I
squeeze(V(:,:,i)) >= 0;
end
to ensure each V_i is positive semidefinite?
variable V(N,N,I) complex semidefinite
declares V(:,:,i) to be complex semidefinite for each i from 1 to I, so there is no further constraint statement required to make each of those hermitian semidefinite (positive semidefinite if complex is not specified).