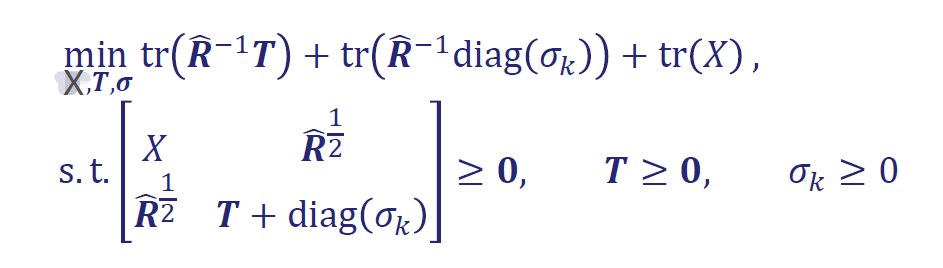A convex programming problem

1

I am regenerating the results of a paper published in IEEE transactions in Array signal processing where they used CVX to solve a convex optimization problem. They are minimizing the following function

bbbbbbbbbbbbbb
bbbbbbbbbbbbbb.png943×268 14.3 KB

among them,R^-1Is the known matrix of the input,T is hermitian toeplitz matrix, X is complex matrix.

I tried many ways to formulate this problem using CVX. none of them scceeded.
e.g.

cvx_begin sdp

variable delta_k(sensor_num,1) ;
variable T(sensor_num,sensor_num) hermitian toeplitz ;
variable X(sensor_num,sensor_num) complex ;

minimize (trace(R_tlide_invT)+trace(R_tlide_invdiag(delta_k))+trace(X))

subject to

[X , R_tlide_half ; R_tlide_half , T+diag(delta_k)] == hermitian_semidefinite(2*sensor_num);
T == hermitian_semidefinite(sensor_num);
diag(delta_k)== semidefinite(sensor_num);

cvx_end

But I obtain following error

Error using minimize (line 36)
Disciplined convex programming error:
Cannot minimize a(n) complex affine expression.

Error in CVX_fun(line 26)
minimize (trace(R_tlide_invT)+trace(R_tlide_invdiag(delta_k))+trace(X)) .

I dont know how to solve this. Can some one help?
Sincere thanks

2

Your objective function does not evaluate to a real (scalar). It’s as simple as that.

Sometimes an expression would be real if computed in exact arithmetic, but given roundoff error from double precision calculations, has a roundoiff level imaginary component, which needs to be eliminated, either by calculation rearrangement, or by taking the real part, in order to avoid a CVX error message.

However, in your case, this is not just a matter of roundoff level imaginary component. As I do not know what was presented in the paper, I don’t know what problem formulation was intended or how it was implemented in CVX. However, one possibility is that the objective function us supposed to be the real part of what is in your code. If that is the case, you can apply the real operator to your objective function. That will be accepted by CVX, but I can’t tell you whether that is the correct implementation of whatever model, which I dontt what t is, is presented in the paper.

1 Like