Wish List: Allow Limited DCP Non-Compliance as Front End for Non-Convex Solvers

21

Hello, I have encountered a new problem again. Now I have simplified my original optimization problem, but I don’t understand why the value of K changes slightly, sometimes it is solvable, sometimes it prompts “”, and sometimes it prompts. I am really anxious, how can I get a stable solution? could you give me some suggestions, thank you very much!

%NEWMODEL
T=0.01;

K=6;
N=2;
M=16;
Bn=180000;
R=21e4+1e4rand(K,1);%随机产生每个用户的数据量
L=zeros(K,N,M);
L(:,1:N,:)=TBn;
L(:,N+1,:)=TBn/2;
[SNR_USV_BS,SNR_DF]=Multirelay_OFDMA_channelmodel_byhh(K,N,M,Bn);

alpha_eq=zeros(K,N+1,M);
for k=1:K
for n=1:N
for m=1:M
alpha_eq(k,n,m)=SNR_DF(k,n,m);
end
end
end
for k=1:K
for m=1:M
alpha_eq(k,N+1,m)=SNR_USV_BS(k,m);%表示选择直接通信所对应的信噪比
end
end

J=0;
cvx_begin
cvx_solver mosek
cvx_expert true %
variables E(K,N+1,M);
variable rou(K,N+1,M) binary;

J=sum(sum(sum(E)));
% for k=1:K

minimize(J)
subject to
sum(sum(rou,1),2)<=1;
R(k)<=sum(sum(L.*(-rel_entr(rou,(rou+E.*alpha_eq))),2),3);
E>=0;

cvx_end

p=zeros(K,N,M);
for k=1:K
for n=1:N+1
for m=1:M
if rou(k,n,m)==0
p(k,n,m)=0;
else
p(k,n,m)=E(k,n,m);
end
end
end
end

22

Having very large numbers such as BnandR can make numerical solution of the optimization problem challenging and precarious. You should try to improve your formulation to avoid that.

After doing 6that, if you still have difficulties, perhaps you can show the solver and CVX output for the various values of K so that forum readers have something specific to look at.

23

OK,so you mean that I should try to give some smaller value to this variable?But that values are more reasonable in my model.I’ll think about that, if I still have difficulties, I will show the solver and CVX output for the various values of K, thanks very much!

24

Choose units for variables so that non-zero values are not very many orders of magntiude from one. The exact solution of the optimization problem may be invariant to the choice of units, but the practical performance of double prevision solvers called by CVX is not.

25

Thank you for the last answer! I would like to ask that in my question, p is clearly restricted to be non-negative. Why do some p obtained after solving this problem take negative values? But in fact, I am more concerned about the product of p and rho. From the results, p corresponding to rho is 0 can take a negative value, and p corresponding to rho is 1 is positive, which should not affect my final result. But I still don’t understand why cvx does not apply non-negative constraints to all p as I wrote.
my optimization problem as follows, many thanks!

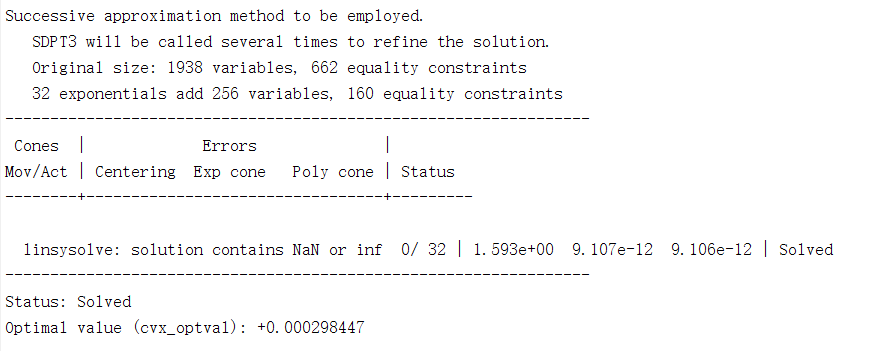
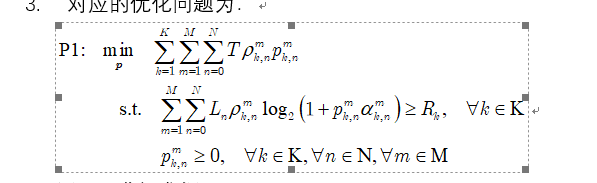image
image881×489 8.9 KB

image

26

Does CVX report the problem is solved to optimality? What is the largest magnitude negative value of an element of p? The solvers are allowed to provided optimal values which violate constraints within a solver tolerance amount.

Also, in the future, please copy and paste code, and use Preformatted text icon. Do not post images of code.

27

Thank you for the last answer! I would like to ask that in my question, p is clearly restricted to be non-negative. Why do some p obtained after solving this problem take negative values? But in fact, I am more concerned about the product of p and rho. From the results, p corresponding to rho is 0 can take a negative value, and p corresponding to rho is 1 is positive, which should not affect my final result. But I still don’t understand why cvx does not apply non-negative constraints to all p as I wrote.
my optimization problem as follows, many thanks!

image
image881×489 8.9 KB

image

28

OK, I got it.Yes, cvx status is ''solved", as follwed,

image
image877×351 8.91 KB

And the value of p is as folows, and I think they aren’t within a solver tolerance, right?
image
image604×634 6.94 KB

29

Why is that called val rather than p? Anyhow, I don’t understand why those values are as large magnitude negative as they are. Do you still have large input data values? That could adversely affect things, including constraint tolerances.

30

Actually, there is no data that has a very large value.Maybe alpha_eq with 1e3 magnitude are too large?
Besides, when I click on the variable name, all variables are displayed like this, as you can see, val, in fact, they have their own names .
It seems that it is not very easy to use cvx well :smiley:

31

I lost track of exactly which output and results go with which code.

Have you tried running the exact same problem and input data, but with Mosek (and CVX 2.2)? If so, what happened? If not, please do so.

32

OK, I think this negative values may won’t affect the correct result of the problem for the time being .I’ll try the mothod you provided tomorrow.Thank you very much!

33

Hi Mark, last time I consulted you, you suggested that I try to solve it in cvx2.2 and mosek. After I specified mosek as the cvx_solver, p no longer has a negative value. It seems that the non-negative constraint is working, I don’t know the specific reason ,may be that there is a binary variable rho in my model, but actually rho is a known binary matrix, not a variable that cvx needs to solve.
Now, for the same problem, I want to ask how to solve the following optimization problem. I tried to write it in cvx, the code is as follows. Could you please help me to answer why it sometimes causes problems infeasible when R increases. In my intuitive opinion, cvx can increase the power p to meet the R constraint, isn’t it?
Besides, there is another problem. In the process of writing the code, I found that writing the constraint in the form of matrix dot multiplication sometimes causes the constraint to not work? Would the for loop be better? What do you think?Will this have an impact?

cvx_begin
cvx_solver mosek
% variable E(K,N+1,M);
variable p(K,N+1,M);
expression  L_off_k(K,1) ;%每个USV在所有子载波上的卸载数据总量
for k=1:K
    for n=1:N+1
        for m=1:M
%            J=J+T_real*rho(k,n,m)*E(k,n,m);
              J=J+T_real*rho(k,n,m)*p(k,n,m);
        end
     end
 end
 minimize(J)
 for k=1:K
 L_off_k(k)=0;
   for n=1:N+1
        for m=1:M
                 L_off_k(k)=L_off_k(k)+L_three(k,n,m)*log(1+rho(k,n,m)*p(k,n,m)*alpha_eq(k,n,m))/log(2);
%               L_off_k(k)=L_off_k(k)+L_three(k,n,m)*log(1+E(k,n,m)*alpha_eq(k,n,m))/log(2);
        end
    end
end

subject to
for k=1:K
    L_off_k(k)>=R(k);
end

% R<=sum(sum(L_three.*(-rel_entr(rho,(rho+E.*alpha_eq)))/log(2),2),3);
% sum(sum(L_three.*rho.*log(1+p.*alpha_eq)/log(2),2),3)>=R;
% for k=1:K
%     for n=1:N+1
%         for m=1:M
%             p(k,n,m)>=0;
%         end
%     end
% end
% E>=0;
p>=0;
cvx_end
34

Regarding feasibility, have you tried removing the objective function and the code calculating j from your code. That turns it into a pure feasibility problem, which can’t be affected by bad numerics associated with the objective function. if you do so, does the problem remain feasible when R is increased.

Because forum readers don’t have the input data, we are kind of operating in the blind. if you showed all solver and CVX output, perhaps a Mosek expert (employee, not me) can assess something.

Also look at https://yalmip.github.io/debugginginfeasible/ except for section 1.

35

Sorry, I forgot to provide my optimization problem.Could you please help me check how to solve the following optimization problem? Is there any error in my code in the last reply?
image

36

I don 't see anything obviously wrong. Keep in mind, though, that if the input data has bad scaling, that essentially amounts to a practical mistake, even though the code itself may not have errors.

37

So how should I judge the quality of the input data? It’s really difficult. You mean that if I encounter an unsolvable situation, first let the other input data remain unchanged,and let the objective function be 0, instead of calculating it using other variables, and then see if the problem is solvable, right?

38

If there is no objective or calculations needed only for the objective, that eliminates the potential for bad (large) numbers in the objective to couple into numerically “bad stuff” happening with the constraints. Therefore, the determination of feasibility may be more reliable when there is no objective function.

You still haven’t shown us the Mosek and CVX output. When R is very large, perhaps it is so large that it is causing difficulties in the solver, either directly due to R, or by causing p, inside the log, to have to be too large for the solver to reliably handle? Are there any warning messages from Mosek?

39

Hi, Mark, I’ll show the output of mosek this time,You know,In my model, I want to observe the change in the total energy consumption (J) of the system as the value of K increases, which is my objective function. In my simulation experiment just now, K only increased to 3 (iter=2), then the problem showed an infeasible state. Can you help me see what might be wrong? In the following, I first gave the output message by mosek, then gave the program to call cvx to solve the problem, and finally gave the called program.

Calling Mosek 9.1.9: 128 variables, 61 equality constraints
   For improved efficiency, Mosek is solving the dual problem.------------------------------------------------------------
MOSEK Version 9.1.9 (Build date: 2019-11-21 11:34:40)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86
Problem
  Name                   :                 
  Objective sense        : min             
  Type                   : CONIC (conic optimization problem)
  Constraints            : 61              
  Cones                  : 32              
  Scalar variables       : 128             
  Matrix variables       : 0               
  Integer variables      : 0     
   Optimizer started.
  Presolve started.
   Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries                  : 1                 time                   : 0.00            
Lin. dep.  - tries                  : 1                 time                   : 0.02            
Lin. dep.  - number                 : 0               
Presolve terminated. Time: 0.03    
Problem
  Name                   :                 
  Objective sense        : min             
  Type                   : CONIC (conic optimization problem)
  Constraints            : 61              
  Cones                  : 32              
  Scalar variables       : 128             
  Matrix variables       : 0               
  Integer variables      : 0               

Optimizer  - threads                : 2               
Optimizer  - solved problem         : the dual        
Optimizer  - Constraints            : 1
Optimizer  - Cones                  : 32
Optimizer  - Scalar variables       : 96                conic                  : 96              
Optimizer  - Semi-definite variables: 0                 scalarized             : 0               
Factor     - setup time             : 0.00              dense det. time        : 0.00            
Factor     - ML order time          : 0.00              GP order time          : 0.00            
Factor     - nonzeros before factor : 1                 after factor           : 1               
Factor     - dense dim.             : 0                 flops                  : 1.21e+02        
ITE PFEAS    DFEAS    GFEAS    PRSTATUS   POBJ              DOBJ              MU       TIME  
0   1.3e+00  2.2e+01  7.7e+00  0.00e+00   -8.665567086e+00  -2.825557343e-05  1.0e+00  0.05  
1   1.9e-01  3.1e+00  2.7e+00  -8.86e-01  -1.281219119e+01  -1.469627065e-04  1.4e-01  0.16  
2   5.4e-02  9.1e-01  1.3e+00  -8.84e-01  -2.350021625e+01  -4.522521056e-04  4.2e-02  0.17  
3   1.6e-02  2.6e-01  7.2e-01  -8.99e-01  -6.647293726e+01  -1.489285667e-03  1.2e-02  0.17  
4   3.0e-03  5.1e-02  2.8e-01  -9.20e-01  -2.549126365e+02  -6.748211881e-03  2.3e-03  0.17  
5   1.4e-03  2.4e-02  1.8e-01  -8.25e-01  -4.390900660e+02  -1.397029864e-02  1.1e-03  0.19  
6   5.2e-04  8.7e-03  1.2e-01  -8.92e-01  -1.407704433e+03  -3.629429828e-02  4.0e-04  0.19  
7   1.7e-04  2.8e-03  6.4e-02  -9.78e-01  -4.184601863e+03  -1.109075233e-01  1.3e-04  0.19  
8   6.1e-05  1.0e-03  3.3e-02  -9.14e-01  -8.339314206e+03  -2.663743644e-01  4.7e-05  0.20  
9   2.3e-05  3.9e-04  1.7e-02  -8.42e-01  -1.587874569e+04  -6.371182135e-01  1.8e-05  0.20  
10  5.9e-06  9.8e-05  7.6e-03  -8.06e-01  -4.818665635e+04  -2.236085978e+00  4.5e-06  0.22  
11  1.6e-06  2.7e-05  3.4e-03  -7.67e-01  -1.297504560e+05  -7.240383509e+00  1.2e-06  0.22  
12  5.5e-07  9.2e-06  1.7e-03  -7.02e-01  -2.678993753e+05  -1.902341549e+01  4.2e-07  0.22  
13  2.0e-07  3.4e-06  9.8e-04  -7.36e-01  -6.700222137e+05  -4.780642041e+01  1.6e-07  0.22  
14  7.2e-08  1.2e-06  4.3e-04  -6.58e-01  -9.908338310e+05  -1.106157038e+02  5.6e-08  0.23  
15  2.0e-08  3.4e-07  2.0e-04  -6.21e-01  -2.819515723e+06  -3.353722230e+02  1.6e-08  0.23  
16  7.3e-09  1.2e-07  6.9e-05  -3.80e-01  -2.497266448e+06  -6.725893835e+02  5.7e-09  0.25  
17  2.5e-09  4.2e-08  3.6e-05  -4.49e-01  -5.716457509e+06  -1.574925838e+03  1.9e-09  0.25  
18  3.7e-10  6.2e-09  1.8e-06  8.16e-02   -6.461665847e+05  -2.991847347e+03  2.8e-10  0.25  
19  2.3e-10  3.9e-09  1.3e-06  -6.10e-01  -9.221866387e+05  -3.783466115e+03  1.8e-10  0.25  
20  2.0e-10  3.3e-09  1.1e-06  1.22e+00   -8.114770991e+05  -3.925218608e+03  1.5e-10  0.27  
21  3.0e-11  5.1e-10  5.7e-08  1.27e+00   -1.024980505e+05  -4.382861691e+03  2.4e-11  0.27  
22  2.8e-12  4.7e-11  1.6e-09  1.02e+00   -1.335392882e+04  -4.465710922e+03  2.2e-12  0.28  
23  6.0e-14  1.0e-12  4.7e-12  1.01e+00   -4.626110954e+03  -4.456392202e+03  4.7e-14  0.28  
Optimizer terminated. Time: 0.33    


Interior-point solution summary
  Problem status  : DUAL_INFEASIBLE
  Solution status : DUAL_INFEASIBLE_CER
  Primal.  obj: -5.3077270987e-05   nrm: 5e-03    Viol.  con: 6e-30    var: 3e-10    cones: 2e-13  
Optimizer summary
  Optimizer                 -                        time: 0.33    
    Interior-point          - iterations : 23        time: 0.28    
      Basis identification  -                        time: 0.00    
        Primal              - iterations : 0         time: 0.00    
        Dual                - iterations : 0         time: 0.00    
        Clean primal        - iterations : 0         time: 0.00    
        Clean dual          - iterations : 0         time: 0.00    
    Simplex                 -                        time: 0.00    
      Primal simplex        - iterations : 0         time: 0.00    
      Dual simplex          - iterations : 0         time: 0.00    
    Mixed integer           - relaxations: 0         time: 0.00    

------------------------------------------------------------
Status: Infeasible
Optimal value (cvx_optval): +Inf

And my input parameters are as follows,

close all
T=1000;
N=4;
M=32;
B=5000000;
Bn=B/M;
T_real=T/Bn;%×Üʱ¼ä
[SNR_USV_BS,SNR_DF]=Multirelay_OFDMA_channelmodel_byhh(14,N,M,Bn);
J_opt=zeros(6,1);
J_greedy=zeros(6,1);
Rmin=15*T*ones(14,1);
for iter=1:6
    K=2+iter-1;
 alpha_eq=zeros(K,N+1,M);
for k=1:K
    for n=1:N
       for m=1:M
       alpha_eq(k,n,m)=SNR_DF(k,n,m);
       end
    end
end
for k=1:K
     for m=1:M
       alpha_eq(k,N+1,m)=SNR_USV_BS(k,m);
     end
end
L_three=zeros(K,N+1,M);
L_three(:,1:N,:)=T/2;
L_three(:,N+1,:)=T;

[J_greedy(iter),p_greedy,rho_greedy,L_off_greedy]=greedy_by_cvx(K,N,M,T_real,Rmin,alpha_eq,L_three);

And the called code is as follows,

function[J,p,rho,L_off_k]=greedy_by_cvx(K,N,M,T_real,R,alpha_eq,L_three)
J=0;%objective function
rho=newmodel_greedy(K,N+1,M,alpha_eq);
cvx_clear
cvx_begin
cvx_solver mosek
variable p(K,N+1,M);
expression  L_off_k(K,1) ;
for k=1:K
    for n=1:N+1
        for m=1:M
              J=J+T_real*rho(k,n,m)*p(k,n,m);
        end
    end
end
minimize(J)
for k=1:K
    L_off_k(k)=0;
    for n=1:N+1
        for m=1:M
L_off_k(k)=L_off_k(k)+L_three(k,n,m)*log(1+rho(k,n,m)*p(k,n,m)*alpha_eq(k,n,m))/log(2);
        end
    end
end
 
subject to
for k=1:K
    L_off_k(k)>=R(k);
end
 
p>=0;
cvx_end
40

Your problem is most likely slightly infeasible.