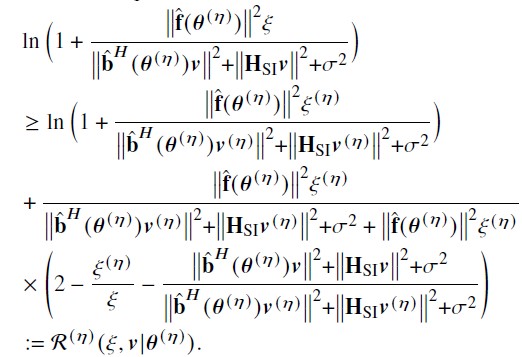I don’t know what’s what.
Please show the mathematical description (formulation) of the problem you are having difficulty with, along with the mathematically RIGOROUS PROOF that that problem is a convex optimization problem. Your description of the problem should make clear what symbols are input data to that problem, and which are optimization variables, and should make clear and explicit, any relationships, explicit or implicit, among any of the symbols. If images in the paper don’t satisfy these criteria, you need to supplement them with additional information.
Sir, I am doing mistakes in writing basic equations only Sir.
for the expression norm(x) ^2, in cvx tool, I am writing only norm{x,2}. Hence, it is not satisfying all the constraints which results in infeasible solution. I will try to rectify it first and then ask questions if any occurs.
Just now , I am trying to modify the mistake done previously. I think I may get the proper solution Now.
Thanks for your patience Sir
norm(x)^2 should be written for CVX as square_pos(norm(x)).
norm(x,2) is the same as norm(x), because the 2-norm is the default norm.
This is the objective function:
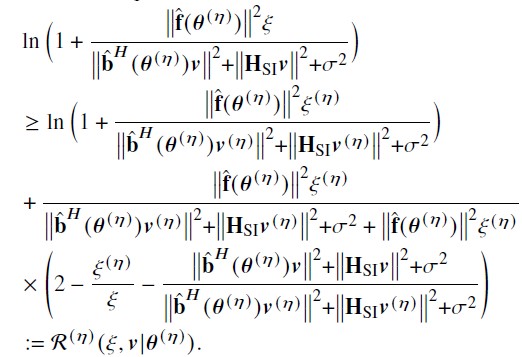
The corresponding code is as follows:
% Compute objective function
f_theta = f + a_u*diag(h)phase_initial;
b_theta = (b_u + a_udiag(d_u)*phase_initial) + (b_d’ + phase_initial.‘*diag(d_d)*a_d’);
obj_1 = log ( 1 + ((f_theta'*f_theta)*P_UE_initial)/( square_pos(norm(b_theta*Tx_beamforming_initial)) + square_pos(norm(h_s_i*Tx_beamforming_initial)) + sigma_sqr ) );
obj_2 = ((f_theta'*f_theta)*P_UE_initial)/( square_pos(norm(b_theta*Tx_beamforming_initial)) + square_pos(norm(h_s_i*Tx_beamforming_initial)) + sigma_sqr + (f_theta'*f_theta)*P_UE_initial ) ;
div1 = (square_pos(norm(b_theta*Tx_beamforming)) + square_pos(norm(h_s_i*Tx_beamforming)) + sigma_sqr);
div2 = square_pos((norm(b_theta*Tx_beamforming_initial)) + square_pos(norm(h_s_i*Tx_beamforming_initial)) + sigma_sqr);
%obj_3 = (2 - (P_UE_initial *inv_pos(P_UE)) - (div1./div2));
obj_3 = ( 2 - (P_UE_initial*inv_pos(P_UE)) - ( square_pos(( norm(b_theta*Tx_beamforming)) + square_pos(norm(h_s_i*Tx_beamforming)) + sigma_sqr) ./square_pos((norm(b_theta*Tx_beamforming_initial)) + square_pos(norm(h_s_i*Tx_beamforming_initial)) + sigma_sqr) ) );
obj = obj_1 + obj_2 * obj_3;
Giving error at obj_3 as follows:
Error using +
Disciplined convex programming error:
Illegal operation: {convex} - {convex}
Error in - (line 21)
z = plus( x, y, true, cheat );
Error in RIS_FD_ISAC_Opt_trial (line 270)
obj_3 = ( 2 - (P_UE_initialinv_pos(P_UE)) - ( square_pos(( norm(b_thetaTx_beamforming)) + square_pos(norm(h_s_iTx_beamforming)) + sigma_sqr) ./square_pos((norm(b_thetaTx_beamforming_initial)) + square_pos(norm(h_s_i*Tx_beamforming_initial)) + sigma_sqr) ) );
Please help me in this regard. And interestingly same code is running on MATLAB 2022a, but not on 2023a. I do not understand the reason behind this one.
Type in the individual terms at the command line and see what CVX says. Have you looked at the “coefficients”. Do they have the same values in the “same” codes you are running on two different MATLAB versions.
The problem with the CVX version not with the MATLAB version Sir.
Version 2 is giving result and using version 3, problem is not running (Showing errors).
I think some syntax (or) rules has been changed for latest version…
Anyway, problem is running with old version for sub-problem-1. Now I have to look for next sub problem with the same version.
CVX pdf book is same for version 2 and version 3???
CVX 3.0beta is riddled with bugs, which are very unlikely to ever be fixed. Do not use it.
Use the latest build of CVX 2.2.
I am using cvx-1.22.zip for my current problem.
What is the difference between these two versions
cvx-1.22.zip and cvx-1.22.tar.gz
And these two are for free solvers only.
I am not getting even after reading license page Sir.
My program is working after downloading free solver and that to
cvx-1.22.zip . Can I use [
cvx-1.22.tar.gz ???
CVX 1.22 is an ancient version from 2012. cvx-1.22.zip is the WINDOWS version; cvx_1.22.tar.gz is the gzipped tar file for Linux. But don’t use CVX 1.22 unless you need to due to having an ancient version of MATLAB.
Use CVX 2.2, downloaded at Download CVX | CVX Research, Inc. .
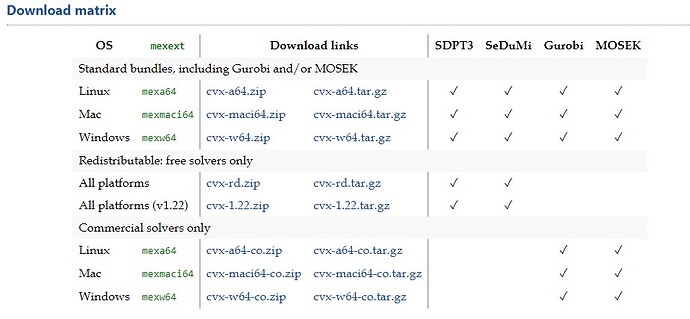
Sir, I am not getting where cvx 2.2 is there in the following as there is no name with CVX 2.2.
Please tell me which one is suitable exactly from the below figure:
And, I am using MATLAB 2022a & MATLAB 2023a
The first 3 lines. Pick the one for your operating system.
Sir, that is version 3. I downloaded and verified also already.
Free solvers only : All platforms (v1.22) is Version 2 Sir.
Remaining all are showing as version 3
Version 3 is elsewhere. cvx-1.22.zip is CVX version 1.22, not CVX 2.2.
Issue the command
cvx_version
to clearly see what version of VCX is installed.
Here is a direct link to CVX 2.2 for WINDOWS: http://web.cvxr.com/cvx/cvx-w64.zip
But it is not suitable for my optimization problem Sir.
My optimization code is running and giving proper results in the CVX 1.22 version only.
The same code is not running (even running, giving improper results) for both CVX 2.2 and cvx 3
Please show us all solver and CVX output from both CVX 1.22 and CVX 2.2, as well as any evidence of the results from 1.22 being proper and the results from 2.2 being improper. Forget about CVX 3.0beta,. because it is full of bug, and ts results should not be relied on.
Yes Sir. We have got same results as given in our base paper and results are reasonable also according to the fundamental knowledge regarding the data rate concept.
For your reference, The solvers and output of the optimization problem using cvx 1.22 is given as follows:
Calling sedumi: 87 variables, 32 equality constraints
For improved efficiency, sedumi is solving the dual problem.
SeDuMi 1.21 by AdvOL, 2005-2008 and Jos F. Sturm, 1998-2003.
Alg = 2: xz-corrector, Adaptive Step-Differentiation, theta = 0.250, beta = 0.500
eqs m = 32, order n = 37, dim = 94, blocks = 12
nnz(A) = 461 + 0, nnz(ADA) = 490, nnz(L) = 261
it : by gap delta rate t/tP t/tD* feas cg cg prec
0 : 9.02E+15 0.000
1 : 1.68E+15 3.01E+15 0.000 0.3334 0.9000 0.9000 1.83 1 1 9.8E+02
2 : 1.96E+14 1.20E+15 0.000 0.4000 0.9000 0.9000 1.78 1 1 3.0E+02
3 : -3.03E+14 5.60E+14 0.000 0.4653 0.9000 0.9000 0.93 1 1 1.6E+02
4 : -3.34E+14 2.78E+14 0.000 0.4971 0.9000 0.9000 0.67 1 1 8.7E+01
5 : -6.58E+14 1.33E+14 0.000 0.4788 0.9000 0.9000 0.35 1 1 6.0E+01
6 : -4.03E+14 5.84E+13 0.000 0.4379 0.9000 0.9000 0.44 1 1 3.0E+01
7 : -5.63E+14 2.28E+13 0.000 0.3906 0.9000 0.9000 0.23 1 1 1.8E+01
8 : -3.37E+14 7.72E+12 0.000 0.3385 0.9000 0.9000 0.29 1 1 8.0E+00
9 : -2.42E+14 2.83E+12 0.000 0.3673 0.9000 0.9000 0.35 1 1 3.9E+00
10 : -9.86E+13 1.05E+12 0.000 0.3691 0.9000 0.9000 0.63 1 1 1.7E+00
11 : -4.28E+13 4.31E+11 0.000 0.4118 0.9000 0.9000 0.88 1 1 8.6E-01
12 : -1.38E+13 1.74E+11 0.000 0.4041 0.9000 0.9000 1.01 1 1 5.2E-01
13 : -6.84E+12 4.18E-17 0.000 0.0000 0.9000 0.7636 1.02 1 1 5.2E-02
14 : -1.78E+12 4.88E-18 0.000 0.1168 0.0000 0.9000 1.01 1 1 1.7E-02
15 : -2.65E+12 1.44E-23 0.000 0.0000 0.9000 0.2086 1.00 1 1 1.5E-05
16 : -3.81E+11 2.75E-24 0.000 0.1908 0.9000 0.9000 1.00 1 1 2.9E-06
17 : -7.26E+10 5.56E-25 0.000 0.2025 0.9062 0.9000 1.00 3 3 6.2E-07
18 : -1.96E+10 1.72E-25 0.000 0.3088 0.9007 0.9000 1.00 3 3 1.9E-07
Run into numerical problems.
iter seconds digits cx by
18 0.1 Inf -3.3265171649e+10 -1.9594854373e+10
|Ax-b| = 3.3e+09, [Ay-c]_+ = 0.0E+00, |x|= 1.2e+16, |y|= 2.2e+02
Detailed timing (sec)
Pre IPM Post
0.000E+00 7.812E-02 0.000E+00
Max-norms: ||b||=12333172332065484, ||c|| = 2,
Cholesky |add|=1, |skip| = 0, ||L.L|| = 19.8968.
Status: Inaccurate/Solved
Optimal value (cvx_optval): -1.95949e+10
The optimal power of UE is:
0.0048
The optimal transmit beamforming vector is:
1.0e-06 *
0.0964 + 0.0296i
-0.0277 + 0.0044i
0.0610 - 0.0015i
0.0003 + 0.0129i
0.1121 - 0.0269i
I wouldn’t rely on the correctness of the result from the CVX 1.22 SeDuMi output. The solver prematurely stopped due to numerical problems, CVX reported the solution as being inaccurate/solved, the optimal objective value has huge magnitude, the optimal vector is of tiny magnitude, and the max norm of b is gargantuan.
In summary, the model and scaling s atrocious from a numerical standpoint. I’d consider the results to be very untrustworthy. With a model and data which is so bad numerically, perhaps any little difference in CVX or solver processing, such as from a different version, could drastically change the results. I don’t know how the results in your base paper were obtained, but I wouldn’t automatically assume that they are necessarily the gold standard of scientific and engineering virtue.
Can you show the output from CVX 2.2? If you have Mosek available, try using that as solver under CVX 2.2, and see what warnings or error messages it produces - I expect there would be some, and you should pay heed to those.
Actually the result that I have sent is the result of last iteration and I have run it for 10 iterations and it is being converged for the 4th iteration only.
I do not know in detail regarding the solver and norm values that you are saying. You may be correct as you are expert in it Sir.
But with cvx 2.2 version, the same problem results in Infeasible even though there is no errors in it.
As I told you, your model and data is numerically terrible. All results with all solvers are probably unreliable, and that includes an assessment of whether a problem is infeasible.
Given you use of an iterative method, any tiny difference in solution of one problem could result in a completely different path for the overall algorithm. Perhaps the inputs and outputs to the problem in each iteration are getting wilder and wilder, until at some point the solver either encounters numerical difficulties or the problem becomes or is assessed (whether correctly or incorrectly) to be infeasible. So this might be why your problem is numerically atrocious. It’s not that there’s anything wrong with CVX 2.2, or that CVX 1.22. is “better” than CVX 2.2., it is probably that your overall algorithm is unreliable and might b essentially inadequate to solve the problem you wish to solve. Just because that algorithm was published in a paper doesn’t mean it’s any good - its success might be highly dependent on the exact problem instance (input data), starting point used, and details of the implementation (presuming you implemented it correctly, which I do not assume to be the case).
You might be lucky if the overall algorithm converges to anything, let alone the global, or even a local optimum of the original problem.
As I wrote at
https://twitter.com/themarklstone/status/1586795881168265216
Don’t apply crude, unsafeguarded (no Trust Region or Line Search) Successive Convex Approximation (SCA) to a new problem … unless your name happens to be Stephen Boyd.
There’s a reason high quality non-convex nonlinear optimization solvers are more than 10 lines long.
If you nevertheless choose to do so, it is at your own peril.