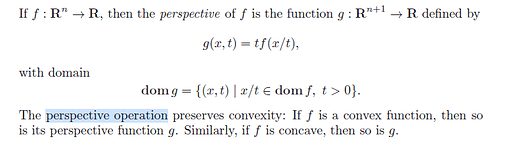Hello~ Mr. Mark. Regard to the Dm^3/Tm^2, I have proved it is convex. As f=(Dm)^3 is convex,
According to the perspective operation of convex function,
the perspective function of f is g=Tm*(Dm/Tm)^3, which is also convex where Dm/Tm belongs to the f domain. (Dm and Tm are real and non-negative)
The reason of f=Dm^3 (sqrt((x1-x2)^2+(y1-y2)^2)^3) is convex is that
[x1,x2,y1,y2]
H[x1,x2,y1,y2]’ (this equals 6*[x1-x2)^2+(y1-y2)^2)^3]) is always larger or equal to 0 when these 4 variables are real and non-negative, where H is the Hessian matrix of function f.
So, is there any way to express this in cvx? If still no, can I use the lower bound to replace this?
I will defer to @Michal_Adamaszek or someone else to address this.
Thank you for this! Mark~
First define variable Dm(M,1), then change
to Dm(i)>=norm(qm(i+1,:)-qm(i,:));. then expressing Dm^3/Tm^2 will do your job.
1 Like
Thank you for your help Jack. But Tm is a affine variable, could we do the division of the affine in CVX?
Please follow Mark’s advice above to express Dm^3/Tm^2.
Actually Mark’s advice cannot handle this as my expression in fact is ||qm+1-qm||^3/Tm^2. Thank you Jack, I am currently trying just dividing this expression to see whether could work or not.
Hello Mark. I recently used this “rotated_lorentz(1)” way to express ||qm+1 - qm||^3/Tm^2 like this:
variables qm(M+1,2) Tm(M,1) temp1(M,1) temp2(M,1)
for i=1:M
{qm(i+1,:)-qm(i,:),temp2(i),Tm(i)} == rotated_lorentz(1);
{temp2(i),temp1(i),qm(i+1,:)-qm(i,:)} == rotated_lorentz(1);
end
Then use temp1 in place of ||qm+1 - qm||^3/Tm^2. What do you think, is that right?
You have implicitly constrained qm(i+1,:)-qm(i,:) >= 0, and have nothing which does what norm does. it appears that you are trying to generalize @Michal_Adamaszek’s formulation for a scalar argument in a way which is not valid. Your qm(i+1,:)-qm(i,:) is not even a scalar, as it is in @Michal_Adamaszek’s formulation.
yes exactly, I am still stuck in this problem.
For the record, here is the formulation for norm(y)^3/x^2, as provided by @Michal_Adamaszek at How to reformulate this in a CVX way
Declare a variable t , add the constraint geo_mean([t,x,x])>=norm(y), and use t in place of norm(y)^3/x^2
Yes thank you Mark, I see. Thank you very much!