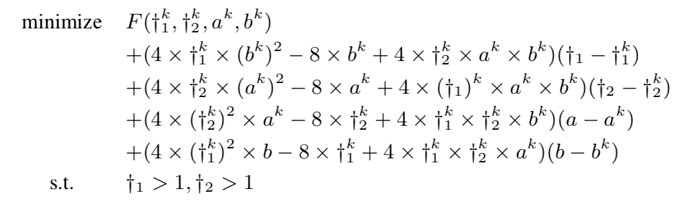Why cvx is not solving this "sequential convex approximation" problem?

1

56%20AM
Screen Shot 2019-09-25 at 10.19.56 AM.png1036×336 19.1 KB
Hello everyone, I am trying to use cvx to solve an optimization problem that relies on the “sequential convex approximation” method (the mathematical formulation is attached):

But I am getting the following error:
Status: Unbounded
Optimal value (cvx_optval): -Inf

Can you help me please in detecting the error? I am attaching the code below:

Code:

cvx_clear
clc
clear all
% tolerance and maxinum number of iterations
tolX = 1e-3;
maxiter = 10;
n=4;
X=zeros(10,4)
for k=1:maxiter
    cvx_begin
    variable Tgt1(1);
    variable Tgt2(1);
    variable a(1);
    variable b(1);   

 X(1,:)= [1.2,1.2,1.0409,0]; 

Phi= (2*X(k,1)^2*X(k,4)^2 + 4*X(k,1)*X(k,2)*X(k,3)*X(k,4) - 8*X(k,1)*X(k,4) + 2*X(k,2)^2*X(k,3)^2 - 8*X(k,2)*X(k,3) + 10)+(2*X(k,4)*(X(k,2)*X(k,3) + X(k,1)*X(k,4) - 1) + 2*X(k,4)*(X(k,2)*X(k,3) + X(k,1)*X(k,4) - 3))*(Tgt1-X(k,1))+(2*X(k,3)*(X(k,2)*X(k,3) + X(k,1)*X(k,4) - 1) + 2*X(k,3)*(X(k,2)*X(k,3) + X(k,1)*X(k,4) - 3))*(Tgt2-X(k,2))+(2*X(k,2)*(X(k,2)*X(k,3) + X(k,1)*X(k,4) - 1) + 2*X(k,2)*(X(k,2)*X(k,3) + X(k,1)*X(k,4) - 3))*(a-X(k,3))+(2*X(k,1)*(X(k,2)*X(k,3) + X(k,1)*X(k,4) - 1) + 2*X(k,1)*(X(k,2)*X(k,3) + X(k,1)*X(k,4) - 3))*(b-X(k,4))
 
%objective function
minimize Phi

    %constraints
        subject to
            Tgt1 >= 1.1
            Tgt2 >= 1.1
cvx_end
X(k+1,:)=[Tgt1 Tgt2 a b]
end
2

Already, using that starting value of X, the problem in the first outer iteration (k=1) is unbounded. You need to diagnose why.

3

Thank you Mr. Stone for your reply, I think that the trust region is missing in my optimization problem. Therefore, when I am minimizing a linear function, it is obvious that the output should be -Inf.

For this I changed the code by defining a vector that includes all the variables and I included a trust region in the constraints.

Can you please let me know if the way I wrote the trust region is correct? Thank you in advance:

Code:
cvx_clear
clc
clear all

% tolerance and maxinum number of iterations
tolX = 0.2;
maxiter = 50;

n=4;
X=zeros(maxiter,4)
%k=1
for k=1:maxiter
cvx_begin
variables x(n) ;%x=[Tgt1 Tgt2 a b]

X(1,:)= [1.1,1.5,0.01,0.1];

Phi= (2X(k,1)^2X(k,4)^2 + 4X(k,1)X(k,2)X(k,3)X(k,4) - 8X(k,1)X(k,4) + 2X(k,2)^2X(k,3)^2 - 8X(k,2)X(k,3) + 10)+(2X(k,4)(X(k,2)X(k,3) + X(k,1)X(k,4) - 1) + 2X(k,4)(X(k,2)X(k,3) + X(k,1)X(k,4) - 3))(x(1,1)-X(k,1))+(2X(k,3)(X(k,2)X(k,3) + X(k,1)X(k,4) - 1) + 2X(k,3)(X(k,2)X(k,3) + X(k,1)X(k,4) - 3))(x(2,1)-X(k,2))+(2X(k,2)(X(k,2)X(k,3) + X(k,1)X(k,4) - 1) + 2X(k,2)(X(k,2)X(k,3) + X(k,1)X(k,4) - 3))(x(3,1)-X(k,3))+(2X(k,1)*(X(k,2)X(k,3) + X(k,1)X(k,4) - 1) + 2X(k,1)(X(k,2)*X(k,3) + X(k,1)X(k,4) - 3))(x(4,1)-X(k,4))

%objective function
minimize abs(Phi)

%constraints
    subject to
    
        x(1,1) >= 1.1
        x(2,1) >= 1.1
       norm(x'-X(k,:))<=10/k

cvx_end
%stop condition
if norm(x’-X(k,:))<=tolX
break;
end
X(k+1,:)=[x(1,1) x(2,1) x(3,1) x(4,1)]
end

4

Well, you seem to have implemented a (two-norm) ball constraint about the previous solution. However your choice of 10/k for the RHS seems rather dubious, at best. That doesn’t appaer to be a very robust trust region formulation. However, this forum is not in the business of designing non-convex optimization (outer) algorithms, so you are on your own. You may be better off just using an-off-the-shelf non-convex optimizer, rather than trying to concoct your own “poor man’s” version, which will likely be vastly inferior.