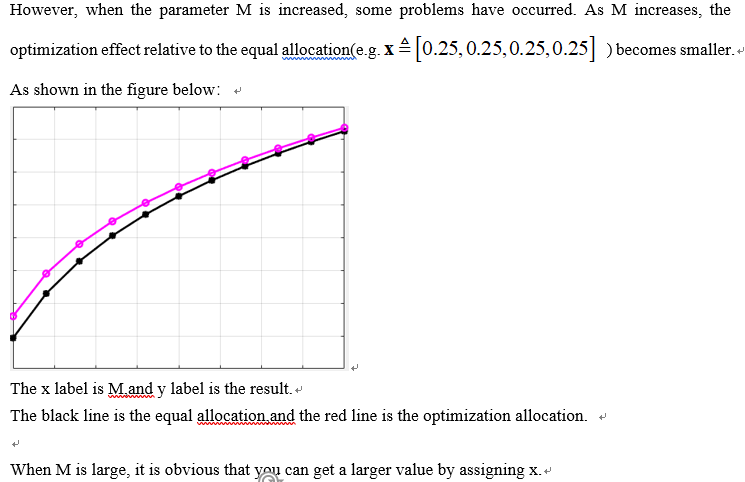
Why can’t CVX find the optimal value when M gets large? Is it because the algorithm cannot be accurately estimated?
CVX’s responsibility is to solve the GP problems you provide it. If the Status is reported as Solved, then it is presumed that CVX solved the problem you provided to it. if you have evidence that any such problem is reported Solved, but not actually solved to optimality within solver tolerance, please present that evidence.
As to how well the iterative algorithm you presents solves the overall non-convex optimization, that is not really a CVX matter, and its detailed diagnosis really outside the scope of this forum. Note that there are plenty of iterative schemes for non-convex problems which don’t necessarily converge to anything, and if they do converge, they don’t necessarily converge to a local optimum, let alone a global optimum. The performance of these algorithms may depend on input data (parameters), such as your M. Simplistic stopping criteria, such as in your algorithm, don’t necessarily serve as reliable optimality criteria, so use at your peril.
If you do solve GP’s with CVX, I recommend you use CVXQUAD CVXQUAD: How to use CVXQUAD's Pade Approximant instead of CVX's unreliable Successive Approximation for GP mode, log, exp, entr, rel_entr, kl_div, log_det, det_rootn, exponential cone. CVXQUAD's Quantum (Matrix) Entropy & Matrix Log related functions although that might not necessarily help whatever difficulty you have been encountering.