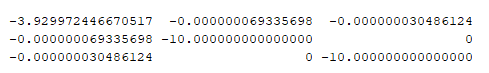What is causing the final Status: Inaccurate/Solved? and how can I modify my code to get it Solved?

1

I can’t figure out why the result I get has status inaccurate/solved.

I have the following optimization problem:
image

I have formulated the above optimization problem as follows:

T=0.1;
B=10^6;
K= 2;
N= 2;
NumberOfUsersInSubcarrier (1:N)=0;
NOMA_max = 2;
UE_SCid (1:K) = 0;
R_max = 140;
L = 15 * 10^4;
B_sub = B/N;
z = 10^-28; % effective capacitance coefficient
C = 10^2; % number of CPU cycles required per bit

for i=1:K
CG (i) = complex(randn(1),randn(1))/sqrt(2); % exponential random distribution with mean value 1
end

for i=1:K
SC_id = randi(N);
while (NumberOfUsersInSubcarrier(SC_id)>=NOMA_max) % each SBS can serve up to NOMA_max_users*N users
SC_id = randi(N);
end
NumberOfUsersInSubcarrier(SC_id)=NumberOfUsersInSubcarrier(SC_id) + 1;
UE_SCid (i) = SC_id; % save the UE’s subcarrier
end

cvx_begin
variable p(2)
variable l(2)
variable r(2)

minimize sum(z*C^3*pow_p(l,3)/T^2+p*T)

subject to
    r >= (L-l)./(B_sub*T)   % Rate constraint
    p >= 0                  % Power constraint
    l >= 0                  % Local data constraint 1
    l <= L                  % Local data constraint 2

    % MAC contraints
    r(1) <= log(1+p(1)*norm(CG(1))^2)
    r(2) <= log(1+p(2)*norm(CG(2))^2)
    r(1)+r(2) <= log(1+p(1)*norm(CG(1))^2 + p(2)*norm(CG(2))^2)

cvx_end

After running the problem I get the following message result:

>> cvx_code
CVX Warning:
_ Models involving “log” or other functions in the log, exp, and entropy_
_ family are solved using an experimental successive approximation method._
_ This method is slower and less reliable than the method CVX employs for_
_ other models. Please see the section of the user’s guide entitled_
_ The successive approximation method_
_ for more details about the approach, and for instructions on how to_
_ suppress this warning message in the future._
_ _
Successive approximation method to be employed.
_ For improved efficiency, SDPT3 is solving the dual problem._
_ SDPT3 will be called several times to refine the solution._
_ Original size: 29 variables, 10 equality constraints_
_ 3 exponentials add 24 variables, 15 equality constraints_
-----------------------------------------------------------------
_ Cones | Errors |_
Mov/Act | Centering Exp cone Poly cone | Status
--------±--------------------------------±--------
_ 2/ 2 | 7.550e+00 4.276e+00 0.000e+00 | Inaccurate/Solved_
_ 2/ 2 | 2.650e+00 4.322e-01 0.000e+00 | Solved_
_ 2/ 2 | 9.921e-02 6.676e-04 0.000e+00 | Solved_
_ 2/ 2 | 1.059e-02 7.579e-06 0.000e+00 | Solved_
_ 0/ 0 | 1.288e-03 0.000e+00 0.000e+00 | Inaccurate/Solved_
_ 0/ 0 | 1.268e-04 0.000e+00 0.000e+00 | Inaccurate/Solved_
_ 0/ 0 | 1.752e-04 0.000e+00 0.000e+00 | Inaccurate/Solved_
-----------------------------------------------------------------
Status: Inaccurate/Solved
Optimal value (cvx_optval): +67.8698

Can someone please help me with what might be the cause of the Inaccurate/Solved status and what should I do in order to reach a solved status?

2

I think Inaccurate/solved is resulting because of the poor scaling n the problem. In particular ,z = 1e-28 is causing difficulty in the objective function, because it makes the first additive term in the objective function of vastly different order of magnitude than the second term. As a result, the variable l is not well determined numerically to the solver. So as is, the optimal objective value is determined fairly well, but l is not well determined at all.

If z is chosen substantially larger, then the problem becomes better behaved.

Given your use of log, I advise you to follow the advice in CVXQUAD: How to use CVXQUAD's Pade Approximant instead of CVX's unreliable Successive Approximation for GP mode, log, exp, entr, rel_entr, kl_div, log_det, det_rootn, exponential cone. CVXQUAD's Quantum (Matrix) Entropy & Matrix Log related functions . In particular, change the MAC constraints to

r(1) <= -rel_entr(1,1+p(1)*norm(CG(1))^2)
r(2) <= -rel_entr(1,1+p(2)*norm(CG(2))^2)
r(1)+r(2) <= -rel_entr(1,1+p(1)*norm(CG(1))^2 + p(2)*norm(CG(2))^2)

However, this does not fix the Inaccurate/solved issue. You need to change z to do that.

1 Like
3

You were absolutely right. I have made the changes to the code you recommended and I have also changed the value of z to 10^-16 based on your suggestions and the final status now is always ‘Solved’. Thanks a million!

However I am having another problem which I think is relevant to this topic, therefore I will ask here instead of opening another thread.

The final values of p after the cvx has been solved, are always greater or equal to zero (which has been set as one of the constraint) and the maximum value I have gotten after running my code 1 million times was more or less around 2000. However, after adding another constraint for the maximum value of p:

p <= P_max

where P_max = (zC^3L^3)/(T^2) = 33750000, I thought this constraint could not possibly cause any problems since the value of p always ends up to be significantly lower than that. But instead, now the final status has become:

Status: Failed
Optimal value (cvx_optval): NaN

and the final p values of the failed convex game end up being:

p =

1.0e+07 *

3.3749
0.0002

I can’t understand how this constraint is causing the cvx problem to fail, especially since the P_max has been set so high which should not cause any changes at all based on the greatest value of p when no maximum limit constraint has been set. Can someone share some wisdom pleeease?

4

Large input numbers anywhere in your problem specification can cause problems for the solvers called by CVX. it is true that the theoretical so0lution is unaffected by adding a non-binding constraint to what was the optimal solution, But doing so can cause havoc with solvers. Either use a relatively small magnitude bound constraint, or don;t use a bound constraint at all.

5

I have a question.
When the problem has good scaling, the ‘log’ is automatically approximated by the solver, e.g., SeDuMi.
Is there possible that the Successive approximation method employed for the ‘log’ function may result in the inaccurate\solved solution?

6

The the Successive approximation method is unreliable. Poor numerical scaling exacerbates the unreliability.

Always try to have good numerical scaling. If possible, use CVX 2.2 with Mosek 9.x. If Mosek is not available to you, follow the advice in the link in my first post of this thread,

7

OK. I will have a try.

8

Hello, I am facing the same problem and I know something wrong with me codes but I could not figured it out how to fix it.
I am trying to reconstruct my object from speckle pattern through cvx optimization .
for i=1:size(S_rand,2)

a=reshape(S_rand(:,i), [520 520]); %% this is my speckles 520*520 matrix 
figure(1)
imagesc(a)
xlabel('X ');
ylabel('Y ');
title(' Speckle pattern through MMF');

pause(0.1)

end
%% cropperd from center 3030
a1=a(1:30,1:30);%% centered cropped speckles 3030 matrix
figure(2);
imagesc(a1);
ylabel(‘Y’)
xlabel(‘X (\mum)’)
set(gca, ‘FontSize’, 10);
title(’ Centered Cropped Submatrix’);
xlabel(‘X (\mum)’);
ylabel(‘Y (\mum)’);
set(gca, ‘FontSize’, 10);

%% %% for 1objects randomly scattered;
minPositionX = 1;
maxPositionX = 20;
minPositionY = 1;
maxPositionY = 20; % Adjust this value based on your requirements

% Number of objects to scatter randomly
num_objects = 5;

% Generate random positions for the objects
positionsX = randi([minPositionX, maxPositionX], 1, num_objects);
positionsY = randi([minPositionY, maxPositionY], 1, num_objects);

% Initialize the o_test matrix

o_test_1 = zeros(length(a1)); %% my object with 30*30 matrix size

w1 = 1; % Width of the objects
% Loop to place each object at its random position
for i = 1:num_objects
x_position = round((length(a1) -10 - w1) / 2);

o_test_1(x_position : x_position + w1 - 1, positionsY(1)) = 1;

end

%% speckle*object%%

o_Im=a1.*o_test_1;%%

o_Im_norm_1 = o_Im / max(o_Im(:));

%%
% CVX optimization;
n = size(a1, 2);
m = size(a1, 1);

% Define the known measurements (observed image)

% y = o_Im_norm_1(:); %% this is the change which I made if i use as vector this condition would not satisfy a1 * x_L1 == y but before that speckles I used as vector and cvx works perfectly
y = o_Im_norm_1;

cvx_begin
variable x_L1(n m ) %% also made there change instead of (n) ı also add (m) variable because of a1 * x_L1 == y
minimize(norm(x_L1, 1))
subject to
% cvx_check = size(a1 * x_L1(:));

    a1 * x_L1 == y %#ok<NOPTS>

cvx_end

% Retrieve the reconstructed object

o_rec_L_1 = reshape(x_L1, [m, length(a1)]);

% Display the reconstructed object

Please guide me where Im getting wrong.

9

Your CVX code looks very strange. It appears that you are constraining the only optimization variable (x_L1) to be equal to input data (y) You are further constraining a1*x_L1 to be equal to that same input data y. Based on that, unless a1 is the Identity matrix (or the scalar “1”, which is an Ideintiy matrix), I don’t see how this problem would even be feasible. And even if if were feasible, there would be no degrees of freedom (only one feasible solution), so the objective function is irrelevant. Am I misreading your code?

As general advice, for a program which makes some sense, if the solver is experiencing difficulties, such as producing a solution CVX reports to be Inaccurate/Solved: Please show all the CVX and solver output. Also, try another solver. if you have Mosek available, try that, as it is the most numerically robust solver, and has the best diagnostics.

10

I have the similar problem and I also want to consult about it~ My output is as follows:

Calling Mosek 8.0.0.60: 1385 variables, 374 equality constraints
For improved efficiency, Mosek is solving the dual problem.

MOSEK Version 8.0.0.60 (Build date: 2017-3-1 13:09:33)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86

MOSEK warning 710: #8 (nearly) zero elements are specified in sparse col ‘’ (935) of matrix ‘A’.
MOSEK warning 710: #8 (nearly) zero elements are specified in sparse col ‘’ (936) of matrix ‘A’.
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 374
Cones : 38
Scalar variables : 1060
Matrix variables : 1
Integer variables : 0

Optimizer started.
Conic interior-point optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator - tries : 0 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.01
Optimizer - threads : 10
Optimizer - solved problem : the primal
Optimizer - Constraints : 356
Optimizer - Cones : 38
Optimizer - Scalar variables : 1048 conic : 114
Optimizer - Semi-definite variables: 1 scalarized : 325
Factor - setup time : 0.02 dense det. time : 0.00
Factor - ML order time : 0.02 GP order time : 0.00
Factor - nonzeros before factor : 5.73e+004 after factor : 5.75e+004
Factor - dense dim. : 36 flops : 1.33e+007
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 2.6e+000 4.1e+003 2.3e+000 0.00e+000 1.365222263e+003 -2.400000000e-004 1.0e+000 0.05
1 8.3e-001 1.3e+003 4.2e-001 -9.97e-001 -1.371128655e+003 -6.624155720e+002 3.2e-001 0.13
2 1.4e-001 2.2e+002 3.2e-002 -9.76e-001 -1.906146928e+004 -5.216959916e+003 5.5e-002 0.14
3 8.6e-002 1.3e+002 1.6e-002 -8.27e-001 -3.014130460e+004 -8.675035094e+003 3.2e-002 0.16
4 1.1e-002 1.7e+001 1.1e-003 -7.18e-001 -1.047465688e+005 -3.459711530e+004 4.0e-003 0.17
5 2.5e-003 3.8e+000 3.8e-004 1.75e-001 -6.604111410e+004 -3.371586434e+004 9.3e-004 0.17
6 1.0e-003 1.6e+000 2.4e-004 7.19e-001 -3.088542488e+004 -1.695696237e+004 3.8e-004 0.19
7 6.9e-004 1.1e+000 1.9e-004 8.03e-001 -2.031490144e+004 -1.019525419e+004 2.6e-004 0.19
8 4.3e-004 6.7e-001 1.5e-004 8.27e-001 -8.779075420e+003 -2.070097021e+003 1.6e-004 0.20
9 3.1e-004 4.8e-001 1.2e-004 7.58e-001 -7.399927418e+002 4.719950951e+003 1.2e-004 0.20
10 1.8e-004 2.9e-001 8.4e-005 6.79e-001 3.863425319e+003 7.638064769e+003 7.0e-005 0.22
11 6.7e-005 1.0e-001 4.7e-005 7.17e-001 -3.089953438e+002 1.276691464e+003 2.5e-005 0.22
12 1.2e-005 1.8e-002 2.2e-005 9.18e-001 -1.131001584e+002 1.156095895e+002 4.5e-006 0.23
13 2.9e-006 4.5e-003 1.1e-005 1.10e+000 -1.347963800e+001 4.088675263e+001 1.1e-006 0.23
14 1.4e-006 2.2e-003 7.5e-006 1.01e+000 1.545616255e+000 2.940087724e+001 5.3e-007 0.25
15 8.2e-007 1.3e-003 5.7e-006 1.01e+000 3.080223125e+000 1.969609424e+001 3.2e-007 0.25
16 4.8e-007 3.3e-004 2.8e-006 1.01e+000 -3.410799018e+000 1.085903546e+000 8.1e-008 0.27
17 3.7e-007 3.2e-004 2.8e-006 1.02e+000 -3.617455309e+000 6.712918140e-001 7.7e-008 0.27
18 1.4e-007 8.6e-005 1.4e-006 1.00e+000 -7.015431420e+000 -5.828088890e+000 2.1e-008 0.27
19 1.4e-007 8.6e-005 1.4e-006 1.00e+000 -7.015431420e+000 -5.828088890e+000 2.1e-008 0.28
Interior-point optimizer terminated. Time: 0.28.

Optimizer terminated. Time: 0.38

Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : NEAR_OPTIMAL
Primal. obj: -7.0154314200e+000 nrm: 7e+004 Viol. con: 2e+001 var: 2e+001 barvar: 0e+000 cones: 0e+000
Dual. obj: -5.8280888885e+000 nrm: 7e+004 Viol. con: 0e+000 var: 6e-004 barvar: 2e-004 cones: 0e+000
Optimizer summary
Optimizer - time: 0.38
Interior-point - iterations : 20 time: 0.28
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00

Mosek error: MSK_RES_TRM_STALL ()

Status: Inaccurate/Solved
Optimal value (cvx_optval): -21.4505

11

First of all please use Mosek 10.1 instead of the very old 8.0.

General information about numerical issues can be found in:

8 Debugging Tutorials — MOSEK Optimization Toolbox for MATLAB 10.1.17 (Sections 8.1, 8.2)

7 Practical optimization — MOSEK Modeling Cookbook 3.3.0 (From around section 7.2)

12

Thank you very much！I will try it.

13

It does work! Thank you! This help me a lot.

15

I have the similar problem and I also want to consult about it, thanks!

clc;
clear;
%%基本参数
L=5;
H=1;
B_total=2510^6;
B_h=B_total/H;
N0=3.9810^(-21);
P_l=1;
e=10^(-2);
K=2;
G=1;
N=2;
Mx=3;
My=3;
M=9;
%%位置设定
LEO_loc_x=[0,50010^3,0,25010^3,50010^3];
LEO_loc_y=[0,0,50010^3,25010^3,50010^3];
LEO_loc_z=[120010^3,120010^3,120010^3,120010^3,120010^3];
user_loc_x=50010^3rand(1,2);
user_loc_y=50010^3rand(1,2);
user_loc_z=0rand(1,2);
% scatter3([LEO_loc_x,user_loc_x],[LEO_loc_y,user_loc_y],[LEO_loc_z,user_loc_z])
%%信道产生
k_factor=db2pow(10);
L_p=@(wavelength,d)(wavelength/(4pid))^2;
% h_rician=@(L_p,k)sqrt(L_p)sqrt(k/(k+1)) + sqrt(1/(k+1)) * sqrt(1/2) (randn(1,1) + 1irandn(1,1));5 10^(-12)
h_rician=@(L_p,k)(normrnd(sqrt((k)/(2(k+1))),1/(2*(k+1)))+1inormrnd(sqrt((k)/(2(k+1))),1/(2*(k+1))))5 10^(-12);
h=zeros(N,L,M);
for i=1:5
for k=1:2
for q=1:9
d=sqrt((LEO_loc_x(i)-user_loc_x(k))^2+(LEO_loc_y(i)-user_loc_y(k))^2+(LEO_loc_z(i)-user_loc_z(k))^2);
path_loss=L_p(1/(2010^9),d);
h(k,i,q)=h_rician(path_loss,k_factor);
end
end
end
h_1=zeros(N,L,M);
for i=1:5
for k=1:2
d=sqrt((LEO_loc_x(i)-user_loc_x(k))^2+(LEO_loc_y(i)-user_loc_y(k))^2+(LEO_loc_z(i)-user_loc_z(k))^2);
vx=(user_loc_x(k)-LEO_loc_x(i))/sqrt((LEO_loc_x(i)-user_loc_x(k))^2+(LEO_loc_y(i)-user_loc_y(k))^2)(user_loc_x(k)-LEO_loc_x(i))/d;
vy=(user_loc_y(k)-LEO_loc_y(i))/sqrt((LEO_loc_x(i)-user_loc_x(k))^2+(LEO_loc_y(i)-user_loc_y(k))^2);
Vx=;
temp=1;
for q=1:Mx
Vx=[Vx,temp];
temp=tempexp(-1jpivx);
end
Vx=1/sqrt(Mx)Vx;
Vy=[x];
temp=1;
for q=1:My
Vy=[Vy,temp];
temp=tempexp(-1jpivy);
end
Vy=1/sqrt(My)Vy;
V=kron(Vx,Vy);
for q=1:9
h_1(k,i,q)=h(k,i,q)V(q);
end
end
end
h_final=zeros(N,ML);
for i=1:5
for k=1:2
for q=1:9
h_final(k,(i-1)9+q)=h_1(k,i,q);
end
end
end
%%上面的h_final的每一行表示一个用户与所有卫星之间的信道
%%求解
W_=rand(KML,KM*L);
A1=;
A2=;
A3=;
A4=;
A5=;
for i=1:5
if i==1
A1=[A1,eye(9,9)];
A2=[A2,zeros(9,9)];
A3=[A3,zeros(9,9)];
A4=[A4,zeros(9,9)];
A5=[A5,zeros(9,9)];
elseif i==2
A1=[A1,zeros(9,9)];
A2=[A2,eye(9,9)];
A3=[A3,zeros(9,9)];
A4=[A4,zeros(9,9)];
A5=[A5,zeros(9,9)];
elseif i==3
A1=[A1,zeros(9,9)];
A2=[A2,zeros(9,9)];
A3=[A3,eye(9,9)];
A4=[A4,zeros(9,9)];
A5=[A5,zeros(9,9)];
elseif i==4
A1=[A1,zeros(9,9)];
A2=[A2,zeros(9,9)];
A3=[A3,zeros(9,9)];
A4=[A4,eye(9,9)];
A5=[A5,zeros(9,9)];
else
A1=[A1,zeros(9,9)];
A2=[A2,zeros(9,9)];
A3=[A3,zeros(9,9)];
A4=[A4,zeros(9,9)];
A5=[A5,eye(9,9)];
end
end
C1=blkdiag(A1’*A1,A1’*A1);
C2=blkdiag(A2’*A2,A2’*A2);
C3=blkdiag(A3’A3,A3’A3);
C4=blkdiag(A4’A4,A4’A4);
C5=blkdiag(A5’A5,A5’A5);
Q1=(h_final(1,:)).'conj(h_final(1,:));
Q1_1=blkdiag(Q1,zeros(ML,ML));
Q2_1=blkdiag(zeros(ML,ML),Q1);
Q2=(h_final(2,:)).'conj(h_final(2,:));
Q1_2=blkdiag(Q2,zeros(ML,ML));
Q2_2=blkdiag(zeros(ML,ML),Q2);

cvx_begin
variable t
variable W(KML,KML) complex
maximize t
subject to
(-rel_entr(1,1/(B_hN0)real(trace(Q1_1W+Q2_1W))+1)+rel_entr(1,1/(B_hN0)real(trace(Q2_1W_))+1)-(log(exp(1))1/(B_hN0)real(trace(Q2_1(W-W_))))/(1/(B_hN0)real(trace(Q2_1W_))+1))>=t
(-rel_entr(1,1/(B_hN0)real(trace(Q1_2W+Q2_2W))+1)+rel_entr(1,1/(B_hN0)real(trace(Q1_2W_))+1)-(log(exp(1))1/(B_hN0)real(trace(Q1_2(W-W_))))/(1/(B_hN0)real(trace(Q1_2W_))+1))>=t
real(trace(C1W))<=P_l
real(trace(C2W))<=P_l
real(trace(C3W))<=P_l
real(trace(C4W))<=P_l
real(trace(C5*W))<=P_l

    real(W)>=0

cvx_end

=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3

=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3

Calling SDPT3 4.0: 12196 variables, 31 equality constraints

num. of constraints = 31
dim. of sdp var = 24, num. of sdp blk = 12
dim. of linear var = 4059
dim. of free var = 8101 *** convert ublk to lblk

SDPT3: Infeasible path-following algorithms

version predcorr gam expon scale_data
HKM 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime

0|0.000|0.000|1.4e+03|6.1e+03|5.6e+08| 1.274206e+02 0.000000e+00| 0:0:00| chol 1 1
1|0.512|0.913|6.6e+02|5.3e+02|1.2e+07| 1.503482e+02 -8.368921e+02| 0:0:00| chol 1 1
2|0.638|0.489|2.4e+02|2.7e+02|3.2e+06| 3.699953e+02 -1.058279e+03| 0:0:00| chol 1 1
3|0.966|0.952|8.0e+00|1.3e+01|1.1e+05| 3.443707e+02 -7.164495e+02| 0:0:00| chol 1 1
4|0.975|0.787|2.0e-01|2.9e+00|2.2e+04| 3.705221e+01 -3.914234e+02| 0:0:00| chol 1 1
5|0.721|0.307|5.7e-02|2.0e+00|1.8e+04| 1.378878e+01 -3.007867e+02| 0:0:00| chol 1 1
6|0.953|0.910|2.6e-03|1.9e-01|1.6e+03| 3.276415e+00 -2.877933e+01| 0:0:00| chol 1 1
7|1.000|0.592|1.4e-08|8.4e-02|7.6e+02| 8.421474e-01 -1.436285e+01| 0:0:00| chol 1 1
8|0.987|0.838|5.9e-09|1.7e-02|1.4e+02| 6.169128e-02 -2.500714e+00| 0:0:00| chol 1 1
9|0.984|0.986|1.4e-09|2.2e-03|1.7e+01| 1.933753e-03 -3.967287e-02| 0:0:00| chol 1 1
10|1.000|0.802|2.0e-09|1.2e-03|2.8e+00| 2.451019e-04 -8.736485e-03| 0:0:00| chol 1 1
11|1.000|0.871|2.0e-09|4.1e-04|5.5e-01| 2.388039e-05 -1.123119e-03| 0:0:00| chol 2 2
12|1.000|0.736|4.0e-09|6.3e-04|1.4e-01| 3.273246e-06 -2.762564e-04| 0:0:00| chol 2 2
13|1.000|0.996|1.7e-09|1.7e-04|1.6e-02| 5.882618e-07 9.469744e-06| 0:0:00| chol 2 2
14|1.000|1.000|5.5e-10|1.8e-05|1.3e-03| 1.214511e-06 -6.670955e-06| 0:0:00| chol 6 6
15|1.000|1.000|4.0e-09|1.5e-06|1.1e-04| 9.139673e-08 -5.289981e-07| 0:0:00| chol 2 2
16|1.000|1.000|2.6e-11|1.3e-07|9.2e-06| 3.211349e-09 -4.138372e-08| 0:0:00| chol
linsysolve: Schur complement matrix not positive definite
switch to LU factor. lu 4 1
17|1.000|0.956|1.3e-09|1.1e-08|4.0e-07|-8.719519e-09 -3.694809e-09| 0:0:00| lu 30 4
18|1.000|0.283|7.4e-08|6.6e-10|3.2e-07|-4.318339e-07 -3.046268e-09| 0:0:00| lu 8 4
19|0.613|0.036|6.6e-07|6.0e-10|1.4e-06|-5.767571e-06 -3.000409e-09| 0:0:00| lu 8 ^26
20|0.001|0.003|5.7e-07|1.6e-09|1.5e-06|-6.650360e-06 -3.116617e-09| 0:0:00|
stop: steps too short consecutively

number of iterations = 20
primal objective value = -4.31833875e-07
dual objective value = -3.04626780e-09
gap := trace(XZ) = 3.24e-07
relative gap = 3.24e-07
actual relative gap = -4.29e-07
rel. primal infeas (scaled problem) = 7.42e-08
rel. dual " " " = 6.65e-10
rel. primal infeas (unscaled problem) = 0.00e+00
rel. dual " " " = 0.00e+00
norm(X), norm(y), norm(Z) = 8.5e+02, 3.4e+01, 3.1e+01
norm(A), norm(b), norm(C) = 5.3e+01, 4.0e+00, 2.7e+00
Total CPU time (secs) = 0.31
CPU time per iteration = 0.02
termination code = -5
DIMACS: 1.5e-07 0.0e+00 9.1e-10 0.0e+00 -4.3e-07 3.2e-07

Status: Inaccurate/Solved
Optimal value (cvx_optval): +4.31834e-07

16

The numerical scaling looks horrible. That might be why Inaccurate/Solve occurred. if you can run this with Mosek as solver, you can see whether it issues any warnings. But regardless, you should try to improve the scaling to get all non-zero input data within a small number of orders of magnitude of one. For however good your scaling is or isn’t, Mosek might do better than CVXQUAD with SDPT3, because it is more robust than SDPT3, and has native exponential cone support, which should be better than CVXQUAD’s Pade approximants.

17

Thanks for your help, after using mosek, it warns like this.

CVX Warning:
Models involving “rel_entr” or other functions in the log, exp, and entropy
family are solved using an experimental successive approximation method.
This method is slower and less reliable than the method CVX employs for
other models. Please see the section of the user’s guide entitled
The successive approximation method
for more details about the approach, and for instructions on how to
suppress this warning message in the future.

Using Pade approximation for exponential
cone with parameters m=3, k=3

=====================================
Using Pade approximation for exponential
cone with parameters m=3, k=3

Calling Mosek 9.1.9: 12196 variables, 31 equality constraints

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:34:40)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86

MOSEK warning 710: #2 (nearly) zero elements are specified in sparse col ‘’ (9) of matrix ‘A’.
MOSEK warning 710: #2 (nearly) zero elements are specified in sparse col ‘’ (15) of matrix ‘A’.
MOSEK warning 710: #2 (nearly) zero elements are specified in sparse col ‘’ (16) of matrix ‘A’.
MOSEK warning 710: #2 (nearly) zero elements are specified in sparse col ‘’ (23) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (33) of matrix ‘A’.
MOSEK warning 710: #2 (nearly) zero elements are specified in sparse col ‘’ (36) of matrix ‘A’.
MOSEK warning 710: #2 (nearly) zero elements are specified in sparse col ‘’ (37) of matrix ‘A’.
MOSEK warning 710: #2 (nearly) zero elements are specified in sparse col ‘’ (39) of matrix ‘A’.
MOSEK warning 710: #2 (nearly) zero elements are specified in sparse col ‘’ (40) of matrix ‘A’.
MOSEK warning 710: #2 (nearly) zero elements are specified in sparse col ‘’ (41) of matrix ‘A’.
Warning number 710 is disabled.
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 31
Cones : 12
Scalar variables : 12196
Matrix variables : 0
Integer variables : 0

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 1 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.03
Optimizer terminated. Time: 0.11

Interior-point solution summary
Problem status : DUAL_INFEASIBLE
Solution status : DUAL_INFEASIBLE_CER
Primal. obj: -1.0000000000e+00 nrm: 7e+12 Viol. con: 0e+00 var: 0e+00 cones: 0e+00
Optimizer summary
Optimizer - time: 0.11
Interior-point - iterations : 0 time: 0.06
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00

Status: Unbounded
Optimal value (cvx_optval): +Inf

18

You need to improve the scaling so that there are no near zero elements which Mosek warned about.

Now that you have Mosek, you should replace CVXQUAD’s exponential.m replacement with the original CVX exponential.m .That way, CVQUAD’s Pade approximant won’t be used, and Mosek’s native exponential cone capability will be used instead.

Then follow the directions in Unable to solve convex problem with CVX and MOSEK - #3 by Mark_L_Stone so that you use the latest version of Mosek.

Then run CVX in a new MATLAB session. Then see what Mosek and CVX say about the solution to the problem.

19

Hi,

I’m currently facing the same issue with MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (26) of matrix ‘A’.
Upon reading your response, ‘You need to improve the scaling so that there are no near zero elements which Mosek warned about.’
I also suspect it might be a scaling issue. I’m currently working on solving a quadratic form x^T * A * x, where A is represented in the form of a matrix as shown below. However, I’m unsure how to scale it properly. Simply applying scaling factors such as 10^3 or 10^6 to matrix A still results in the same warning, and sometimes even yields an ‘unbounded’ status. Could you please provide guidance on how to perform the scaling?

figure

Thank you.

20

Perhaps those near zero elements should be exactly zero? Do they arise as the solution to some other problem? It’s your optimization problem, so you should make that assessment.

Perhaps there are also other near zero input data somewhere in your problem?

21

The (3,2), (2,3) elements of matrix A must be exactly zero, and the other should not be zero and there is only data near zero. I’m sorry I don’t understand what this means “Do they raise the solution to some other problem?”