Successive approximation method to be employed.
SDPT3 will be called several times to refine the solution.
Original size: 398 variables, 170 equality constraints
15 exponentials add 120 variables, 75 equality constraints
Cones | Errors |
Mov/Act | Centering Exp cone Poly cone | Status
--------±--------------------------------±--------
11/ 11 | 1.481e+00 1.327e-01 0.000e+00 | Solved
3/ 3 | 2.680e-01 4.370e-03 0.000e+00 | Solved
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Solved
Status: Solved
Optimal value (cvx_optval): +143.367
Successive approximation method to be employed.
SDPT3 will be called several times to refine the solution.
Original size: 398 variables, 170 equality constraints
15 exponentials add 120 variables, 75 equality constraints
Cones | Errors |
Mov/Act | Centering Exp cone Poly cone | Status
--------±--------------------------------±--------
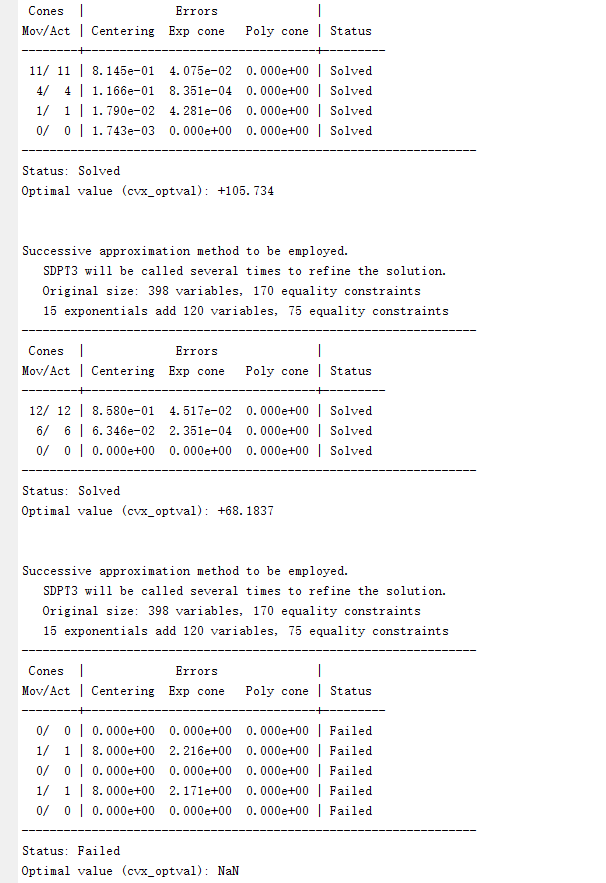
11/ 11 | 8.145e-01 4.075e-02 0.000e+00 | Solved
4/ 4 | 1.166e-01 8.351e-04 0.000e+00 | Solved
1/ 1 | 1.790e-02 4.281e-06 0.000e+00 | Solved
0/ 0 | 1.743e-03 0.000e+00 0.000e+00 | Solved
Status: Solved
Optimal value (cvx_optval): +105.734
Successive approximation method to be employed.
SDPT3 will be called several times to refine the solution.
Original size: 398 variables, 170 equality constraints
15 exponentials add 120 variables, 75 equality constraints
Cones | Errors |
Mov/Act | Centering Exp cone Poly cone | Status
--------±--------------------------------±--------
12/ 12 | 8.580e-01 4.517e-02 0.000e+00 | Solved
6/ 6 | 6.346e-02 2.351e-04 0.000e+00 | Solved
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Solved
Status: Solved
Optimal value (cvx_optval): +68.1837
Successive approximation method to be employed.
SDPT3 will be called several times to refine the solution.
Original size: 398 variables, 170 equality constraints
15 exponentials add 120 variables, 75 equality constraints
Cones | Errors |
Mov/Act | Centering Exp cone Poly cone | Status
--------±--------------------------------±--------
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Failed
1/ 1 | 8.000e+00 2.216e+00 0.000e+00 | Failed
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Failed
1/ 1 | 8.000e+00 2.171e+00 0.000e+00 | Failed
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Failed
Status: Failed
Optimal value (cvx_optval): NaN
Successive approximation method to be employed.
SDPT3 will be called several times to refine the solution.
Original size: 398 variables, 170 equality constraints
15 exponentials add 120 variables, 75 equality constraints
Cones | Errors |
Mov/Act | Centering Exp cone Poly cone | Status
--------±--------------------------------±--------
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Failed
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Failed
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Failed
Status: Failed
Optimal value (cvx_optval): NaN
What are the possible ways to solve this kind of situation where the first few times are solved and the latter is failed