Using cvx to optimize SOCP

1

Hi,
I am new to optimization and am looking to implement this paper using cvx in matlab. The optimization equations are given below:

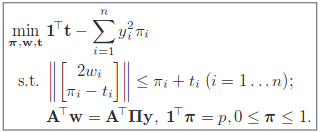
where p is the defined number of outliers which are to be discarded every iteration. My code is given below:

cvx_begin
variable w(n) nonnegative
variable m(n) nonnegative
variable t(n) nonnegative
M = diag(m)
minimize(ones(n,1)’* t - y’* My)
subject to
t >= 0
0 <= m <= 1
sum_square_abs(w) <= m’t %% Error is in this line
A’ w == A’ M*y
ones(n,1)’*m == p
cvx_end

The error I get is:
Error using .* (line 262)
Disciplined convex programming error:
Invalid quadratic form(s): not a square.

Error in * (line 36)
z = feval( oper, x, y );

Error in translation (line 19)
sum_square_abs(m) <= w’*t

Error in main (line 45)
t = translation(pl1_params, pl1_dist, pl2_dist, A_ij, sig)

2

I don’t understand what you were trying to do in the erroneous line.

Enter it “as written” (that’s the beauty of CVX, which really likes second order cones)
for i=1:n, norm([2*w(i);m(i)-t(i)]) <= m(i)+t(i), end

1 Like
3

Oh thank you. I was unsure how to write it.

4

Alternatively, norms can be used in order to avoid the for loop
norms([2*w';(m-t)']) <= (m+t)'

5

i believe that will speed up computations in case of large sizes.