Solving cvx optimisation problem with time varying matrices

1

Dear All,

I need to solve this problem as per screenshot below
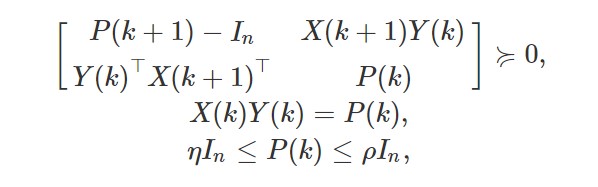Screenshot 2021-07-28 101358 .
The objective is to find the matrices P(k) and Y(k) for k=0,1,2,… N-1 such as the constraints are satisfied. (niu and rho are selected by me depending on the desired accuracy). Since those matrices are time varying, I tried to solve the problem in a loop in this way.

cvx_begin

variable P(n,n,N+1)
variable Y(L,n,N)

for i = 1:N
X_2 = [x1(:,i+1) x2(:,i+1) x3(:,i+1)];
X_1 = [x1(:,i) x2(:,i) x3(:,i)];

 [P(:,:,i+1)-eye(n), X_2*Y(:,:,i); Y(:,:,i)'*X_2', P(:,:,i)] == semidefinite(2*n);
 X_1*Y(:,:,i) == P(:,:,i);
 P(:,:,i) - niu*eye(n) >= 0;
 P(:,:,i) - rho*eye(n) <= 0;

end

cvx_end

However, the code seems not to work and I can’t get a feasible solution. Is it due to the code or more like the model? Because I don’t seem to find a problem.

Thank you in advance

2

I will leave checking of the indexing to you.

I think you need
variable P(n,n,N+1) symmetric
so perhaps CVX is issuing a warning about non-symmetric semidefinite constraints which you might be ignoring?

Also, do you really want

 P(:,:,i) - niu*eye(n) >= 0;
 P(:,:,i) - rho*eye(n) <= 0;

to be element-wise constraints as opposed to semidefinite constraints? Maybe the source you took this from has a typo in using \le instead of \preceq. Note that they are element-wise as entered in CVX because you are not using sdp mode.

No matter which type of constraints those are, the choice of \eta and \rho can obviously affect feasibility.