Dear experts, There is a convex SDP and it can be optimally solved by CVX. But due to the definition of S=x*x' where 'x' is a complex column vector in communication field, the variable ‘S’ in the code below should be a Hermitian semidefinite matric with rank 1 . However, I have no idea to add the constraint of ‘rank(S)=1’. Here is the cvx code without the constraint of ‘rank(S)=1’:

clear,clc;
g_k=0.01;
sigma_2=1.e-13;
n=4;
Q_max=0.1000;
P_max=1;
Beta_k=0.5;
Eta_k=0.5;
h_k=[0.0291 - 0.0047i, 0.0083 - 0.0027i, 0.0138 + 0.0110i, -0.0106 - 0.0028i];
cvx_begin sdp
variable Q_k
variable S(n,n) Hermitian semidefinite
maximize ( g_k.^2/sigma_2 * Q_k )
trace(S) <= P_max
Q_k<= Beta_k * Eta_k * h_k * S * h_k’ ;
Q_k<=Q_max; %#ok
cvx_end
S,Q_k,rank(S)
rank(S)=1 is a non-convex constraint, and can not be explicitly included in a problem presented to CVX.
AS you have seen, CVX may be able to handle a convex relaxation in which the rank constraint is relaxed to a convex constraint or eliminated altogether, or perhaps handled by minimizing a convex proxy, such as the nuclear norm.
Thank you for your help, sir.
Dear experts, I want to use -rel_entr(a,a+p) to solve the problem:
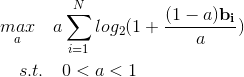
where ‘a’ is a scalar variable, and ‘ b ’ is a known vector. I want to use -rel_entr(a,a+p) to solve the proplem above but I have no idea to solve the different sizes of ‘a’ and ‘p’. The wrong code is shown below.
b = 1.0e-14 * [0.0443 0.0267 0.1469];
cvx_begin
variable a
maximize -rel_entr(a,a*(1-b)+b)
0<a<1
cvx_end
Thanks very much.
Log2(x) = log(x)/log(2) so you can divide by log(2). However, the argmax would be the same even without dividing by log(2).
Change
maximize -rel_entr(a,a*(1-b)+b)
to
maximize(sum(-rel_entr(a,a*(1-b)+b)))
or if you really want log2, to
maximize(sum(-rel_entr(a,a*(1-b)+b))/log(2))
The scaling of your problem may present difficulties. I’ll let you look into that.
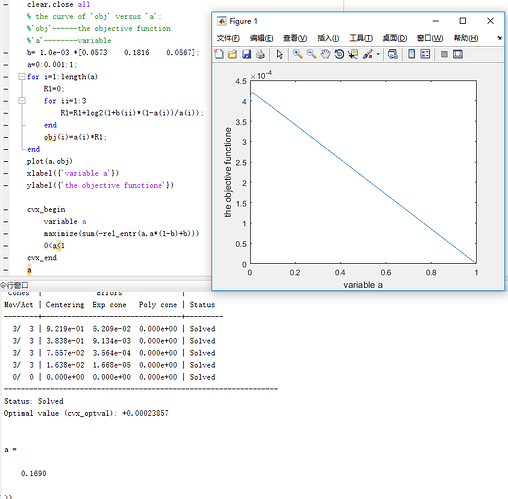
Thank you for your helpful response, sir. But I found that CVX usually mak mistake when the value of vector b is small enough. I plot the curve of the objective function versus variable ‘a’, and it can be easily seen that ‘a’ is around 0.01 when the maximal ‘obj’ is achieved. But CVX got a different optimal value of ‘a’(0.1690) which is obviously wrong. The result and code is shown below.
clear,close all
% the curve of ‘obj’ versus ‘a’;
%‘obj’------the objective function
%‘a’--------variable
b= 1.0e-03 [0.0573 0.1816 0.0567];
a=0:0.001:1;
for i=1:length(a)
R1=0;
for ii=1:3
R1=R1+log2(1+b(ii)(1-a(i))/a(i));
end
obj(i)=a(i)*R1;
end
plot(a,obj)
xlabel({‘variable a’})
ylabel({‘the objective functione’})cvx_begin
variable a
maximize(sum(-rel_entr(a,a*(1-b)+b)))
0<a<1
cvx_end
a
That’is why I wrote
The scaling of your problem may present difficulties. I’ll let you look into that.
You need to improve the scaling of your problem. The solver apparently is not able to deal well with such small values of b.
Also, I rrecommend you install CVXQUAD per CVXQUAD: How to use CVXQUAD's Pade Approximant instead of CVX's unreliable Successive Approximation for GP mode, log, exp, entr, rel_entr, kl_div, log_det, det_rootn, exponential cone. CVXQUAD's Quantum (Matrix) Entropy & Matrix Log related functions . However, given that CVX’s Successive Approximation method appears to have succeeded, i doubt CVXQUAD will make your results come out better in this case, but I don’t know for sure.
Let’s see whether someone clever comes along who can come up with a nice change of variables or something to improve the formulation of the problem.so that the solver is presented a numeriically nicer problem.
I will try your way and carefully check the scalling of the problem.Thanks very much for your help.
Hello! How can you make variable S(N,N) with rank=1 ?