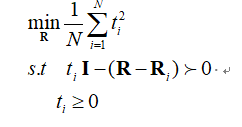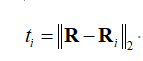SDP constraints must be affine

Nonconvex
1

I am tring to solve the following problem here.
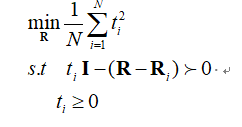
image

where
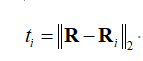
image
There is an error like that:
Error using >= (line 22)
SDP constraints must be affine.

Error in ComputeMeanMatrix_Norm2 (line 17)
ti*eye(N)>=real((R-ReferMatrixs{1,i}))

what’s wrong? Can anybody help?

cvx_begin sdp
variable R(N,N) hermitian
for i=1:num_Matrix
temp=(norm(R-ReferMatrixs{1,i},2));
t=t+(temp);
end
t=t./num_Matrix;
minimize(t)
subject to
for i=1:num_Matrix
ti=(norm(R-ReferMatrixs{1,i},2));
ti*eye(N)>=real((R-ReferMatrixs{1,i}));
ti>=0;
end

cvx_end

2

What’s wrong is that SDP constraints must be affine, but t is not affine. CVX only accepts SDPs which are LMIs: Linear Matrix Inequalities. The matrix appearing in an SDP in CVX must be a linear (affine) function of CVX variables. Norm is not linear.

The semidefinite constraint is (reformulatable to be) convex in one dimension (N = 1), but I doubt it is in dimension >= 2. I will assume it is not convex unless you prove it is,

3

why this constraint is accept by CVX?
image

4

Because it complies with CVX"s DCP rules. Norm of an affine expression is allowed by CVX and is convex. Convex expression <= constant is allowed by CVX and is convex.

When you attempt to use norm in a matrix argument for an SDP (as you did inthe first post of this thread), that is not allowed by CVX, and is not necessarily convex.

Nonlinear SDPs are not allowed by CVX, are generally not convex, and may be difficult to solve even to local optimality.

5

Thanks a lot. I got it. I thought it was convex, but it seems that I need check it out.