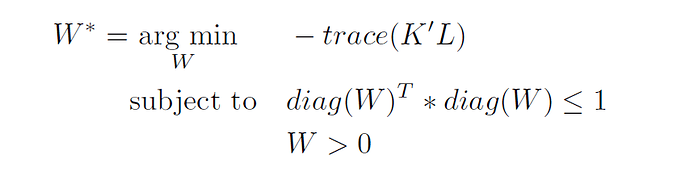Dear community,
I’m new to the field of quadratically constraint quadratic programming (QCQP). In one of my projects, I’m dealing with a domain adaption problem where I need to identify invariant features between two domains X_{S} \in [ x_{1},x_{2},..,x_{n}] and X _{T} \in [ y_{1},y_{2},..,y_{n}] . I came across this Paper:
https://www.cs.cmu.edu/~jgc/publication/Feature%20Selection%20for%20Transfer%20Learning.pdf
where this is solved by using the Maximum Mean Discrepancy (MMD) as a distance measure between both domains. The Distance in RKHS can be computed as follows:
MMD(X_{S} ,X _{T} ) = \Bigg\Vert \cfrac{1}{n_{S}} \sum_{i=1}^{n_{S}}\Phi(X_{S_{i}})-\cfrac{1}{n_{T}} \sum_{i=1}^{n_{T}}\Phi(X_{T_{i}}) \Bigg\Vert^2_{ \mathcal{H}}
X _{S} and X _{T} are data samples from both domains respectively with ns/nT samples. By applying the kernel trick, the problem can be formulated as:
MMD(X_{S} ,X _{T} ) =tr\left(KL\right)
such that
K= \left[ \begin{array}{rrrr} K_{xx} & K_{xy} \\ K_{yx} & K_{yy} \end{array}\right] and L= \left[ \begin{array}{rrrr} L_{xx} & L_{xy} \\ L_{yx} & L_{yy} \end{array}\right]
where K is the Kernel matrix and L a coefficient matrix with:
L_{xx}=\cfrac{1}{n_{S}^2}, L_{yy}=\cfrac{1}{n_{T}^2} and L_{xy}=\cfrac{-1}{n_{S} n_{T}}
By using a diagonal weight matrix W (used for identifying invariant and variant featured) the Kernel (a polynomial Kernel in this example) can be expressed as:
K_{xx}^{'} = ((xW^{1/2})*(xW^{1/2})^{T}+1)^{d} wher d is the dimension of the polynominal kernel
K_{xx}^{'} = (xWx +1)^{d}
K_{yy},K_{xy} and K_{yx} are similarly computed.
The QCQP optimization problem is given by:
I tried to implement the algorithm with the following code:
randn(‘state’,13);
dim =6%the dimesnions of my datase
x = randn(30,dim)%dummy data - x contains m samples from domain 1 and
% n samples from domain 2 -30 samples total
m = 20 % samples from domain 1
n = 10 % samples from domain 2
L = zeros(m+n,m+n) %defining a coefficient matrix for MMD Calculation
L(:,: ) = -1/m*n
L(1:m, 1:m) = 1/(m^2)
L(m+1:end, m+1:end) = 1/(n^2)
cvx_begin
variable W(dim,dim) diagonal%is a diagonal weight matrix
%for selecting invariant features
K = power(x*W*x'+1,2)%using a polynominal kernel 2nd degree
obj = -trace(K*L)%get the objective function
minimize(obj)
subject to%define the constarints
diag(W).'*diag(W)<=1
W > 0
cvx_end
However, it fails with the following message:
Disciplined convex programming error:
Illegal affine combination of convex and/or concave terms detected.
Error in quadobj (line 19)
obj = -trace(QL)%get the objective function*
I just don’t know why the Q*L produces this problem. Could you please explain why my objective function is not convex? As I’m trying to wrap my head around it for a while now, any help/hints would be appreciated. Thank you