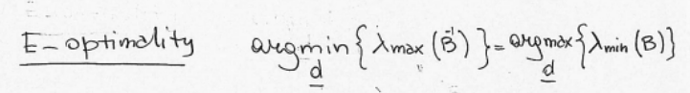One or more output arguments not assigned

1

Hi all, I want to implement a convex-relaxation for the E-optimality design criterion, that is:
By defining
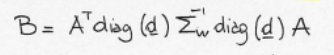
image

the optimization problem would be

image
image.png721×98 25.2 KB

I have implemented in Matlab using this function

function [d] = e_optimality(Uk, s, sigma)
%% E-OPTIMALITY DESIGN CRITERION, CONVEX RELAXATION
%   
%       OUTPUT: sampling_set= vector with ordered sampling
%       set
%
%       INPUT: Uk= NxK Laplacian eigenvector in the selected band
%              s= number of samples
%              sigma: entry noise matrix

N= size(Uk,1);
Sigma= diag(sigma*ones(N,1))
Sigma_inv= inv(Sigma);


cvx_begin
variable d(N)
D= diag(d)
B= Uk'*Sigma_inv* D*Uk;
minimize -lambda_min(B)
subject to
           d*ones(N,1)==s;
           0<=d<=1;
cvx_end

Unfortunately, when launghing the function I have the following error:

One or more output arguments not assigned during call to "varargout".

Error in minimize (line 14)
    x = evalin( 'caller', sprintf( '%s ', varargin{:} ) );

Error in e_optimality (line 20)
    minimize -lambda_min(B)

It seems to be the minimize -lambda_min in CVX causing the problem. What could it be?
Thank you

2

Did you actually look at what CVX produced?

CVX accepted my minimize -lambda_min(B) statement.

Your statement
d*ones(N,1)==s
is erroneous because variable d(N) makes d an N by 1 vector (not 1 by N), so it is not conformal with ones(N,1). So either change it to d'*ones(N,1) or ones(1,N)*d or variable d(1,N) or, more simply. if you can get into the MATLAB mentality and away from the Boyd and Vandenberghe book convention, just use sum(d) == s.

3

Sure, you are right. Anyway, the error persists… the code stops when arriving to the objective function…

4

Please show the complete output from cvx_version , provide a complete reproducible example complete with all input data, as well as all CVX output. Please make the example as small in size as possible, and simplify, if possible, such as not wrapping the CVX code in a MATLAB function, provided that the simplified version still exhibits the error.