Here is my code.
cvx_begin
cvx_solver mosek_2
%优化变量, x1,y1为新的轨迹
variables t x1(101) y1(101)
%设置变量关系
maximize(t)
subject to
e1 = Puh0./a1;
e2 = Puh0./a2;
e3 = Pu*h0./a3;
c1 = P1.*h0./b1;
c2 = P2.*h0./b2;
c3 = P3.h0./b3;
%各用户可达速率的定义
R1ulb = a1.log(1+e1./(H^2+norms([x y]-repmat([s1x s1y],101,1),[],2).^2))./log(2)-a1./log(2).e1./((H^2+norms([x y]-repmat([s1x s1y],101,1),[],2).^2).(H^2+norms([x y]-repmat([s1x s1y],101,1),[],2).^2+e1)).(square_pos(norms([x1 y1]-repmat([s1x s1y],101,1),[],2))-norms([x y]-repmat([s1x s1y],101,1),[],2).^2);
R2ulb = a2.log(1+e2./(H^2+norms([x y]-repmat([s2x s2y],101,1),[],2).^2))./log(2)-a2./log(2).e2./((H^2+norms([x y]-repmat([s2x s2y],101,1),[],2).^2).(H^2+norms([x y]-repmat([s2x s2y],101,1),[],2).^2+e2)).(square_pos(norms([x1 y1]-repmat([s2x s2y],101,1),[],2))-norms([x y]-repmat([s2x s2y],101,1),[],2).^2);
R3ulb = a3.log(1+e3./(H^2+norms([x y]-repmat([s3x s3y],101,1),[],2).^2))./log(2)-a3./log(2).e3./((H^2+norms([x y]-repmat([s3x s3y],101,1),[],2).^2).(H^2+norms([x y]-repmat([s3x s3y],101,1),[],2).^2+e3)).(square_pos(norms([x1 y1]-repmat([s3x s3y],101,1),[],2))-norms([x y]-repmat([s3x s3y],101,1),[],2).^2);
R1vlb = b1.log(1+c1./(H^2+norms([x y]-repmat([d1x d1y],101,1),[],2).^2))./log(2)-b1./log(2).c1./((H^2+norms([x y]-repmat([d1x d1y],101,1),[],2).^2).(H^2+norms([x y]-repmat([d1x d1y],101,1),[],2).^2+c1)).(square_pos(norms([x1 y1]-repmat([d1x d1y],101,1),[],2))-norms([x y]-repmat([d1x d1y],101,1),[],2).^2);
R2vlb = b2.log(1+c2./(H^2+norms([x y]-repmat([d2x d2y],101,1),[],2).^2))./log(2)-b2./log(2).c2./((H^2+norms([x y]-repmat([d2x d2y],101,1),[],2).^2).(H^2+norms([x y]-repmat([d2x d2y],101,1),[],2).^2+c2)).(square_pos(norms([x1 y1]-repmat([d2x d2y],101,1),[],2))-norms([x y]-repmat([d2x d2y],101,1),[],2).^2);
R3vlb = b3.log(1+c3./(H^2+norms([x y]-repmat([d3x d3y],101,1),[],2).^2))./log(2)-b3./log(2).c3./((H^2+norms([x y]-repmat([d3x d3y],101,1),[],2).^2).(H^2+norms([x y]-repmat([d3x d3y],101,1),[],2).^2+c3)).(square_pos(norms([x1 y1]-repmat([d3x d3y],101,1),[],2))-norms([x y]-repmat([d3x d3y],101,1),[],2).^2);
%约束条件(22a)和(22b),因为有六个用户,所以分为六个式子0.
B0/(101Rt)sum(R1ulb) >= t;
B0/(101Rt)sum(R2ulb) >= t;
B0/(101Rt)sum(R3ulb) >= t;
B0/(101Rt)sum(R1vlb) >= t;
B0/(101Rt)sum(R2vlb) >= t;
B0/(101Rt)*sum(R3vlb) >= t;
%约束条件(18h)和(18i)
for i=1:100
norm([x1(i+1)-x1(i),y1(i+1)-y1(i)]) <= Dmax
end
x1(101) == x1(1);
y1(101) == y1(1);
cvx_end
After I got the result, x1, y1 is solved. Then I replace square_pos() in R1ulb with .^2. The result should be the same, but it wasn’t. I am very confused. The norm is always positive so square_pos() should equal to .^2. But it wasn’t. Can someone help me?
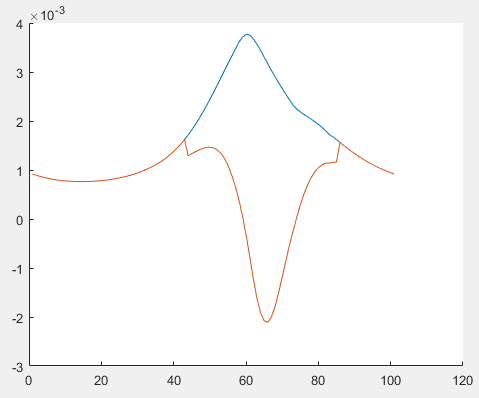
The orange line is R1ulb with square_pos() in cvx. The blue line is R1ulb after i replace square_pos() with .^2.