Issues with a convex SOCP problem

1

Hello,

I am trying to solve the following convex SOCP problem with CVX. My problem is that CVX-status shows “Solved” state but when I check the constraints, they are not satisfied. I was wondering if you can help me to find my mistake here?

%-----load required matrices and vectors----------------------------------
load h
load D1
load D2
load QI

%—values--------------------------------------------
gamma = .1;
R = 6;
Lw = 5;
P1 = 41.14;
P2 = 19.79;

D = P1D1+P2D2+eye(RLw);
h_tild = [0;h];
D_tildq = ([0,zeros(1,RLw);zeros(RLw,1), D])^(.5);
Q1_tildq = ([1,zeros(1,RLw);zeros(RLw,1), P2QI+D1])^(.5);
Q2_tildq = ([1,zeros(1,RLw);zeros(RLw,1), P1*QI+D2])^(.5);
a1 = sqrt(gamma/P2);
a2=sqrt(gamma/P1);

%—optimization----------------------------------------------------
cvx_begin quiet
cvx_precision best
cvx_solver Mosek
variable w(RLw+1) complex
minimize( norm(D_tildqw) )

subject to
    w(1)==1;
    imag(w(2:end)'*h)==0;   %(w'*h_tild)
    real(w'*h_tild) >=  a1*norm(Q1_tildq*w);
    real(w'*h_tild) >=  a2*norm(Q2_tildq*w);

cvx_end

cvx_status

%—check the constraints---------------------------
const1=real( (w’h_tild) - a1(norm(Q1_tildqw)) )
const2=real( (w’h_tild) - a2(norm(Q1_tildqw)) )

Here is the link to the matrices that I am using for this run and also the m-file for this example:

https://drive.google.com/open?id=1Hhg1jeLlP4R9N2FJJ9CcTUIPtXqgopSA

Here is the problem formulation:

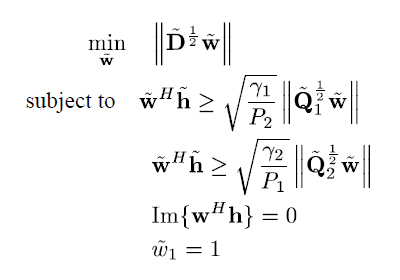
cvx_problem

Any help would be appreciated!

2

What is cvx_status reported as? If the problem has been reported as solved, then

How big are the constraint violations? Solvers allow themselves a tolerance for producing a solution which is not exactly feasible.

3

Cvx_status is “solved”. But instead of getting a positive constraint, the constraint is a very small negative value, for example in the order of -1e-9.
Would you please explain what do you mean by the solver tolerance?
Does it mean the solution is not reliable?

4

That is within solver tolerance of feasibility. If you don’t like that, either adjust the solver feasibility tolerance using cvx_solver_settings http://cvxr.com/cvx/doc/solver.html#advanced-solver-settings (but you can’t make solver feasibility tolerance too small, given use of double precision) or add 1e-6 or 1e-7 (or maybe 2e-8) to the right hand side of the inequality to ensure that the solver solution will be strictly feasible if you really require that.