I have convert my optimization problem into a suitable form so that Cvx can solve it, but still the status shows infeasible, anyone have idea about this?
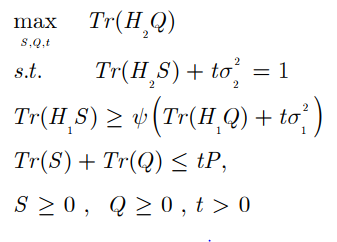
Code i made is;
clear,clc %Clear all
m=2; %number of Tx and Rx antennas
n=1;
P=1; %Transmitted Power
%rng(1);
%H=rand(m,m); %Channel matrix
G1=rand(n,m);
G2=rand(n,m);
W1=rand(m,n);
W2=rand(m,n);
T1=W1W1’;
%t=0.5;
t=1/(trace(G2G2’W1W1’)+1);
%Arho = [0.3 0; 0 0.3]; %Fix Arho
I=eye(m,m) %Identity matrix
%Arhobar=I-Arho %Arhobar
cvx_clear %To clear models used before
cvx_begin %To begin a new CVX model
variable T1(m,m) Symmetric %S Variable
maximize (trace(G2G2’W2W2’)); %Objective Function
subject to
(trace(G2G2’*T1))+t==1;
number of iterations = 5
residual of dual infeasibility
certificate X = 1.14e-27
reldist to infeas. <= 3.44e-28
Total CPU time (secs) = 0.18
CPU time per iteration = 0.04
termination code = 2
DIMACS: 2.8e-09 0.0e+00 8.1e-01 0.0e+00 -1.0e+00 2.0e-05
Status: Infeasible
Optimal value (cvx_optval): -Inf
The trace constraints are not mutually compatible. Various combinations of trace constraints may be feasible, depending on the random input data you generated.
Do you have actual problem inputs, not just random inputs, to test this on?
Feasibility may depend on the inputs. Perhaps “real” data results in a feasible problem, whereas random data generated per the probability distribution you are using, might (usually or always) not be
@Erling, I agree, because what matters is the multivariate probability distribution of the inputs. Real problems tend to have structure which is not manifested in independent uniform or Normal random numbers (everyone on this forum uses rand or randn to generate and populate independent random numbers in an entire matrix or vector).
You still might be able to achieve realistic structure by superimposing random numbers on an imposed structure or sparsity pattern, i.e., you only populate certain elements of a matrix with random numbers.
In fact I did just this on my final project for Gene Golub’s Statistical Computing course in March 1982. Using the for loop (one of the few programming features) and rand capabilities in the original Fortran-based MATLAB, I generated random matrices having specified structure or properties, such as (symmetric) psd (covariance matrices) , correlation matrices (psd matrices constrained to have unit diagonal), Toeplitz, circulant, Hurwitz and other special matrices. I systematically controlled the condition numbers to various specified levels. Then I examined the relation of condition number estimators in various norms to actual condition numbers in various norms. Over 24 years later, about a year and a half before he died,I talked to Golub at a conference. I mentioned that he gave me an A+ on that project. He asked me if I thought I deserved it. I said yes.Those were my last words ever to him. BTW, back in those more innocent (just pre-AIDS) days, long before important applications such as recommending which teen celebrities conservative old geezers should follow on social media, Golub referred in class to SVD as a Stanford social disease.
It sounds like your problem is feasible or not, depending on the input data. The :“solution” to your difficulties is to use real(istic) input data.If that is infeasible, then you need to examine hwo good your mode is.
