i have the following inequality constraints , instead of using a loop , i want to make it in matrix form , how to do that so that both solutions will be same
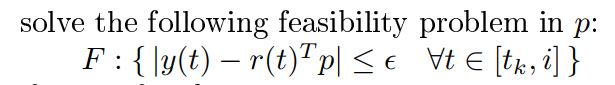
y is a scalar , r and p are vectors
i have the following inequality constraints , instead of using a loop , i want to make it in matrix form , how to do that so that both solutions will be same
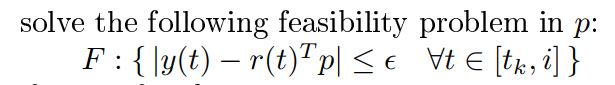
y is a scalar , r and p are vectors
I think if you use a vector y, matrix r, producing a vector y-r'*p, and apply norms to it, that ought to do what you want. I leave the details to you.
applying norms or the abs operator ??
You can apply norms so that the result will be a vector of two-norms, with each two-norm being applied in the dimension which has only a single element, which will therefore be the same as abs.
For instance
cvx_begin
variable x(3)
norms(x,[],2)
ans =
cvx convex expression (3x1 vector)
In your case, apply this to the column vector y - r'*p, in place of my x above, where y is a column vector and r is a suitable matrix.
So
norms(y - r'*p,[],2) <= epsilon
the right hand side should be the one vector times eps i think , coz we have multiconstraints , and what will the norm give on the left hand side
Assume there are n constraints.
y is n by 1. p is m by 1. r is m by n (i.e., an m by 1 column for each constraint).
So y - e'*p is an n by 1 vector.
norms(y - r'*p,[],2) is an n by 1 vector, each element of which is the absolute value of the corresponding element of y - r'*p.
The use of `ones(n,1) on the RHS is optional, and is automatically applied in MATLAB and CVX. I omitted it to reduce clutter in the program.
Actually, abs can be used directly as a more straightforward alternative to norms, and will be applied per element, thereby producing a vector output from a vector input.
abs(y - r'*p) <= epsilon