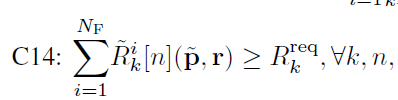
I have no idea what that notation means. I doubt any other forum readers do. And even if we knew what the notation means, we need to know what is input data and which are the optimization (decision) variables.
thankyou reply! The above formula indicates that for any k, n, R > R_req. k,n are know,such as k=3,n=23.R_req is constant. p and r are optimal variable. The code i worte is as follow
delta_t=5;
T=120;
N=T/(delta_t);
K=6;
k1=[-1100,600,0];
k2=[-700,-600,0];
k3=[-400,400,0];
k4=[200,200,0];
k5=[600,1200,0];
k6=[800,-400,0];
w=[k1;k2;k3;k4;k5;k6];
R_1=3e+5*ones(N,1);
R_2=2e+5*ones(N,1);
R_3=4e+5*ones(N,1);
R_4=1e+5*ones(N,1);
R_5=3e+5*ones(N,1);
R_6=2e+5*ones(N,1);
R_req=[R_1,R_2,R_3,R_4,R_5,R_6];
H=100;
Bt=5e+6;
beta=0.001;
p=0.1;
for n=1:1:N
qx1(n,1)=-600+1193.5*(cos((2*pi*(n-1)*delta_t)/(T-delta_t)));
qy1(n,1)=233+1193.5*(sin((2*pi*(n-1)*delta_t)/(T-delta_t)));
end
for n=1:1:N
qz(n,:)=H;
end
qz1=qz;
q1=[qx1,qy1,qz1];
for n=1:1:N
for k=1:1:K
gamma(n,k)=(p*beta)/(((norm(q1(n,:)-w(k,:)))^2)*delta);
end
end
for n=1:1:N
for k=1:1:K
A(n,k)=-p*beta*delta^2*log(e)/((((norm(q1(n,:)-w(k,:)))^2)*delta^2)*((((norm(q1(n,:)-w(k,:)))^2)*delta^2)+p*beta));
end
end
for n=1:1:N
for k=1:1:K
B(n,k)=Bt*log(1+gamma(n,k));
end
end
R_tot1=0;
E_f1=0;
EC1=0;
cvx_begin
variable Q(N,3)
dual variable yy
for n=1:1:N
for k=1:1:K
C(n,k)=A(n,k)*(pow_pos(norm(Q(n,:)-w(k,:)),2)-pow_pos(norm(q1(n,:)-w(k,:)),2));
end
end
for n=1:1:N
for k=1:1:K
ff(n,k)=C(n,k)+B(n,k);
R_tot1=R_tot1+ff(n,k);
end
end
maximize R_tot1
subject to
for k=1:1:K
for n=1:1:N
RR1(n,k)= (ff(n,k));
end
end
yy: RR1>=R_req;
for n=1:1:N
Q(n,3)>=50;
end
cvx_endPlease read http://cvxr.com/cvx/doc/basics.html#assignment-and-expression-holders . You need to declare C, ff, RR1 as expressions. However, all you really need is C.
You can rewrite your program as
cvx_begin
variable Q(N,3)
expression C(K,K)
dual variable yy
for n=1:1:N
for k=1:1:K
C(n,k)=A(n,k)*(pow_pos(norm(Q(n,:)-w(k,:)),2)-pow_pos(norm(q1(n,:)-w(k,:)),2));
end
end
maximize(sum(sum(C+B)))
yy: C + B >= R_req;
Q(:,3) >= 50
cvx_end
You didn’t supply values for delta and e, for which I made up values of delta_t and 2. When i did so, the problem was infeasible due to the constraint C+B>=R_req
As to whether this corresponds to the problem you really want to solve, I have no idea,.
hi! mark, thank you for your replay. i forget an important infromation. The parameter delta= 1.0000e-11; e=2.7182. I have a problem as follow
cvx_begin
variable Q(N,3)
expression C(K,K)
dual variable yy
for n=1:1:N
for k=1:1:K
C(n,k)=A(n,k)(pow_pos(norm(Q(n,:)-w(k,:)),2)-pow_pos(norm(q1(n,:)-w(k,:)),2));
end
end
maximize(sum(sum(a(n,k)(C+B))))
yy: a*(C + B) >= R_req;
Q(:,3) >= 50
cvx_end
a is n*k sparse zero matrix. it is cannot satisfy the constraint, how can i rewrite this constraint.
Using your values of delta and e and the CVX program I listed above, SeDuMi found an optimal solution.
Yes, mark. The previous one can get the optimal solution, but the following code can’t get the optimal solution.
delta_t=5;
T=120;
N=T/(delta_t);
K=6;
k1=[-1100,600,0];
k2=[-700,-600,0];
k3=[-400,400,0];
k4=[200,200,0];
k5=[600,1200,0];
k6=[800,-400,0];
w=[k1;k2;k3;k4;k5;k6];
R_1=1e+7*ones(N,1);
R_2=2e+7*ones(N,1);
R_3=3e+7*ones(N,1);
R_4=1e+7*ones(N,1);
R_5=2e+7*ones(N,1);
R_6=3e+7*ones(N,1);
R_req=[R_1,R_2,R_3,R_4,R_5,R_6];
H=100;
Bt=5e+6;
beta=0.001;
p=0.1;
delta= 1.0000e-11;
e=2.7182;
E_init=3.996e+5;
Vmax=50;
zeta=0.012;
v0=4.3;
M1=4e+7;
M2=Bt*log(1+(p*beta)/(H^2*delta));
R_tot=0;
for n=1:1:N
qx1(n,1)=-600+1193.5*(cos((2*pi*(n-1)*delta_t)/(T-delta_t)));
qy1(n,1)=233+1193.5*(sin((2*pi*(n-1)*delta_t)/(T-delta_t)));
end
for n=1:1:N
qz(n,:)=H;
end
qz1=qz;
q1=[qx1,qy1,qz1];
for n=1:1:N
for k=1:1:K
gamma(n,k)=(p*beta)/(((norm(q1(n,:)-w(k,:)))^2)*delta);
end
end
for n=1:1:N
for k=1:1:K
RR(n,k)=Bt*log(1+gamma(n,k));
end
end
cvx_begin
cvx_solver mosek
variable a(N,K) binary;
for k=1:1:K
for n=1:1:N
R_tot=R_tot+Bt*a(n,k)*RR(n,k);
end
end
maximize R_tot;
subject to
for n=1:1:N
for k=1:1:K
R_req(n,k)-RR(n,k)<=M1*(1-a(n,k))-1;
RR(n,k)-R_req(n,k)<=M2*a(n,k);
end
end
cvx_end
for n=1:1:N
for k=1:1:K
A(n,k)=-p*beta*delta^2*log(e)/((((norm(q1(n,:)-w(k,:)))^2)*delta^2)*((((norm(q1(n,:)-w(k,:)))^2)*delta^2)+p*beta));
end
end
for n=1:1:N
for k=1:1:K
B(n,k)=Bt*log(1+gamma(n,k));
end
end
cvx_begin
variable Q(N,3)
expression C(N,K)
dual variable yy
for n=1:1:N
for k=1:1:K
C(n,k)=A(n,k)*(pow_pos(norm(Q(n,:)-w(k,:)),2)-pow_pos(norm(q1(n,:)-w(k,:)),2));
end
end
for n=1:1:N
for k=1:1:K
ff(n,k)=a(n,k)*(C(n,k)+B(n,k));
end
end
maximize(sum(sum(ff)))
yy: ff >= R_req;
Q(:,3) >= 50
cvx_end
Status: Infeasible
Optimal value (cvx_optval): -Inf
I think the problem lies in yy: ff>= R_req, How do I deal with this sparse matrix?
You apparently are using your first program to produce an optimal binary a as input into your second program. See my now edited post at Hi!How to edit A(m,n)>=B in cvx?A is a sparse Matrix, B is a constant for how to do that.
thankyou! Mark, i will try .