As we know, when A is a hermitian semidefinite matrix, trace(X^HAX) is convex,but cvx can’t deal this expression, so how can i deal with it ? Thank you !
About this question: X^H denotes conjugate transpose operation; X is a matrix; A is a hermitian semidefinite matrix.
trace(X'*A*X) = trace(X'*sqrtm(A)*sqrtm(A)*X) = norm(sqrtm(A)*X,'fro')^2
So use square_pos(norm(sqrtm(A)*X,'fro'))
If it appears by itself in the objective function, there is no need to square, and it is numerically better to use norm(sqrtm(A)*X,'fro'), which has the same argmin.
If A is strictly positive definite, then its Colesky factorization can be used instead of sqrtm(A),resulting in square_pos(norm(chol(A)*X,'fro')) . However, the formulation with sqrtm can always be used.
Thank you very much for you reply, it’s helpful.
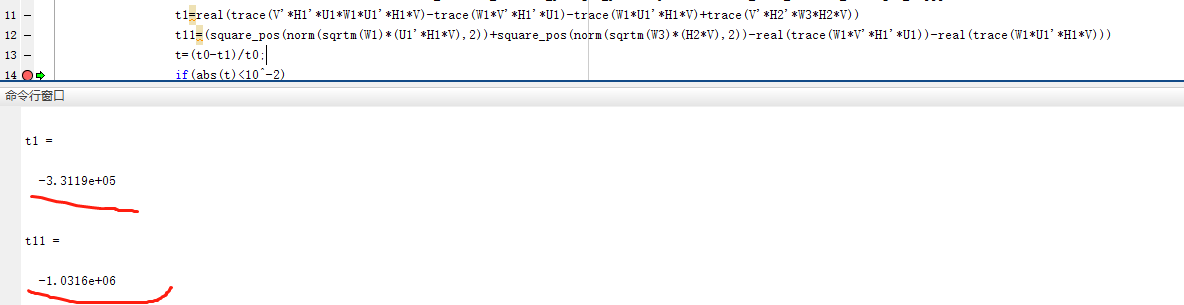
Hi Mark, why these two values are not equal.
t1=real(trace(V'*H1'*U1*W1*U1'*H1*V))
t11=square_pos(norm(sqrtm(H1'*U1*W1*U1'*H1)*V,2))Why should they be? Those expressions aren’t even equal if all the variables are real scalars.
Your formulas do not correspond to what I provided in my first post of this thread.
en, So what shall I do ? I want to express trace(V'*H1'*U1*W1*U1'*H1*V) in cvx, V is variable and H1, U1, W1 are constant matrixs. (H1'*U1*W1*U1'*H1) is hermitian positive semidefinite.
trace(V'*H1'*U1*W1*U1'*H1*V)+trace(V'*H2'*W3*H2*V)-trace(W1*V'*H1'*U1)-trace(W1*U1'*H1*V) this is full expression of my objective function, where V is variable and H1, U1, W1, W3 are constant matrixs and W1, W3 are hermitian positive semidefinite. I’d like to express it in cvx.
W1 and W3 play the role of A in my first post of this thread.
U1'*H1*V and H2*V play the role of X.
Apply one of the reformulaltions in my first post with these correspondences. You will need to do the squaring of the norms, because these terms do not appear by themselves in the objective function.
The final two terms can be entered as is in CVX because the only (CVX) variable, V appears affinely.
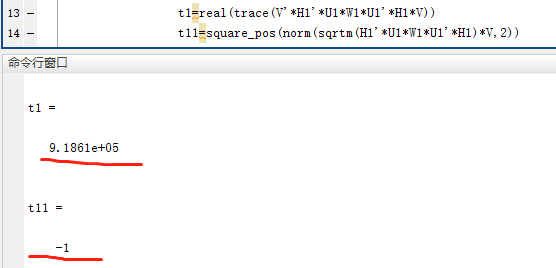
These are the newly values, but they still not equal.
cvx.m as following:
cvx_begin quiet
cvx_solver mosek
variable V(Nt,d0);
minimize (square_pos(norm(sqrtm(W1)*(U1'*H1*V),2))+square_pos(norm(sqrtm(W3)*(H2*V),2))-real(trace(W1*V'*H1'*U1))-real(trace(W1*U1'*H1*V)))
subject to
square_pos(norm(V,2))<=1;
square_pos(norm(sqrtm(H_SP)*V,2))<=Pt*abs(h_PP)^2/kama_p-sigma_p;
2*real(trace(V'*H2'*H2*V0))>=EH0/(epxier*(1-theta))-(square_pos(norm(h_PE+H_IE*G0*h_PI,2))*Pt+sigma_e)+real(trace(V0'*H2'*H2*V0));
cvx_endYou need to use
square_pos(norm(...,,'fro'))
as in my post,
not
square_pos(norm(...,2))
as in your code
The 2-norm and Frobenius norm of a matrix are very different things. https://en.wikipedia.org/wiki/Matrix_norm
It seems the value of square_pos(norm(…,‘fro’)) is -1 or 1.
Please show a complete reproducible example, starting from a fresh MATLAB session. Copy and paste your code into a post.
If square_pos of anything comes out to -1, or any norm of anything is negative, something is wrong. You are probably messing something up.
clc
clear all
M=20;
Nt=5;
Nr=4;
Ne=4;
sigma_s=10^(-9);
sigma_e=sigma_s;
sigma_p=sigma_s;
theta=0.7;
epxier=0.8;
Pt=1;
kama_p=3;
EH0=10^(-7);
d0=3;
H_SI=sqrt(0.5)*(randn(M,Nt)+1j*randn(M,Nt)); %--
H_SS=sqrt(0.5)*(randn(Nr,Nt)+1j*randn(Nr,Nt));% --
H_SE=sqrt(0.5)*(randn(Ne,Nt)+1j*randn(Ne,Nt)); %--
h_SP=sqrt(0.5)*(randn(1,Nt)+1j*randn(1,Nt));% ---
h_PI=sqrt(0.5)*(randn(M,1)+1j*randn(M,1)); %---
h_PS=sqrt(0.5)*(randn(Nr,1)+1j*randn(Nr,1)); %--
h_PE=sqrt(0.5)*(randn(Ne,1)+1j*randn(Ne,1));% --
h_PP=sqrt(0.5)*(randn(1,1)+1j*randn(1,1));%---
H_IE=sqrt(0.5)*(randn(Ne,M)+1j*randn(Ne,M));% ---
H_IS=sqrt(0.5)*(randn(Nr,M)+1j*randn(Nr,M));%---
dx=2.5;
dy=10;
dps=5;
r_SS=8;
r_SE=8;
r_SP=sqrt(dx^2+dps^2);
r_SI=sqrt(dx^2+dy^2);
r_IS=sqrt((dy-r_SS)^2+dx^2);
r_IE=sqrt((dy-r_SE)^2+dx^2);
r_PP=dx;
r_PS=dps+r_SS;
r_PE=dps+r_SE;
r_PI=sqrt(dx^2+(dy+dps)^2);
L0=0.01;
H_SI=H_SI*sqrt(L0*((r_SI)^-2.2));%-
H_SS=H_SS*sqrt(L0*((r_SS)^-2.7));%-
H_SE=H_SE*sqrt(L0*((r_SE)^-2.7));%-
h_SP=h_SP*sqrt(L0*((r_SP)^-2.7));%-
h_PI=h_PI*sqrt(L0*((r_PI)^-2.2));%-
h_PS=h_PS*sqrt(L0*((r_PS)^-2.7));%
h_PE=h_PE*sqrt(L0*((r_PE)^-2.7));%
h_PP=h_PP*sqrt(L0*((r_PP)^-2.7));%-
H_IE=H_IE*sqrt(L0*((r_IE)^-2.2));%-
H_IS=H_IS*sqrt(L0*((r_IS)^-2.2));%-
H_SP=h_SP'*h_SP;
q0=exp(j*2*pi*randn(M,1));
G0=diag(q0);
V0=sqrt(1/(Nt*d0))*exp(j*2*pi*randn(Nt,d0));
H1=H_SS+H_IS*G0*H_SI;
H2=H_SE+H_IE*G0*H_SI;
U1=inv(((h_PS+H_IS*G0*h_PI)*(h_PS+H_IS*G0*h_PI)'*Pt+sigma_s*eye(Nr)+H1*V0*V0'*H1'))*H1*V0;
E1=(eye(d0)-U1'*H1*V0)*(eye(d0)-U1'*H1*V0)'+U1'*((h_PS+H_IS*G0*h_PI)*(h_PS+H_IS*G0*h_PI)'*Pt+sigma_s*eye(Nr))*U1;
W1=inv(E1);
W3=inv((h_PE+H_IE*G0*h_PI)*(h_PE+H_IE*G0*h_PI)'*Pt+eye(Ne)*sigma_e+H2*V0*V0'*H2');
t0=real(trace(V0'*H1'*U1*W1*U1'*H1*V0)-trace(W1*V0'*H1'*U1)-trace(W1*U1'*H1*V0)+trace(V0'*H2'*W3*H2*V0));
while 1 %%%Solve V
cvx_begin quiet
cvx_solver mosek
variable V(Nt,d0)
minimize (square_pos(norm(sqrtm(W1)*(U1'*H1*V),'fro'))+square_pos(norm(sqrtm(W3)*(H2*V),'fro'))-real(trace(W1*V'*H1'*U1))-real(trace(W1*U1'*H1*V)))
subject to
square_pos(norm(V,2))<=1;
square_pos(norm(sqrtm(H_SP)*V,2))<=Pt*abs(h_PP)^2/kama_p-sigma_p;
2*real(trace(V'*H2'*H2*V0))>=EH0/(epxier*(1-theta))-(square_pos(norm(h_PE+H_IE*G0*h_PI,2))*Pt+sigma_e)+real(trace(V0'*H2'*H2*V0));
cvx_end
t1=real(trace(V'*H1'*U1*W1*U1'*H1*V)-trace(W1*V'*H1'*U1)-trace(W1*U1'*H1*V)+trace(V'*H2'*W3*H2*V));
t11=(square_pos(norm(sqrtm(W1)*(U1'*H1*V),'fro'))+square_pos(norm(sqrtm(W3)*(H2*V),'fro'))-real(trace(W1*V'*H1'*U1))-real(trace(W1*U1'*H1*V)));
t1=trace(V'*H1'*U1*W1*U1'*H1*V)
t2=square_pos(norm(sqrtm(W1)*(U1'*H1*V),'fro'))
t=(t0-t1)/t0;
if(abs(t)<10^-2)
break
end
V0=V;
t0=t1;
endI removed the quiet option, so that the solver and CVX output is shown. Everything looks fine. Not at all like whatever it was you showed.
Calling Mosek 9.2.20: 167 variables, 31 equality constraints
For improved efficiency, Mosek is solving the dual problem.
MOSEK Version 9.2.21 (Build date: 2020-9-1 11:11:27)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 31
Cones : 6
Scalar variables : 67
Matrix variables : 2
Integer variables : 0
Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 2
Eliminator terminated.
Eliminator - tries : 1 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.05
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 31
Cones : 6
Scalar variables : 67
Matrix variables : 2
Integer variables : 0
Optimizer - threads : 8
Optimizer - solved problem : the primal
Optimizer - Constraints : 19
Optimizer - Cones : 6
Optimizer - Scalar variables : 57 conic : 56
Optimizer - Semi-definite variables: 2 scalarized : 172
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 184 after factor : 190
Factor - dense dim. : 0 flops : 6.47e+04
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 3.0e+02 6.6e+01 7.0e+00 0.00e+00 5.000421364e+00 -1.000000000e+00 1.0e+00 0.08
1 1.4e+02 3.1e+01 4.8e+00 -1.00e+00 -1.844947876e+01 -2.328952457e+01 4.6e-01 0.22
2 3.1e+01 6.9e+00 2.3e+00 -1.00e+00 -8.173476644e+01 -7.910941386e+01 1.0e-01 0.22
3 6.9e+00 1.5e+00 1.1e+00 -1.00e+00 -1.558770785e+01 2.169598180e+01 2.3e-02 0.23
4 1.6e+00 3.6e-01 5.2e-01 -1.00e+00 1.295306038e+03 1.471660036e+03 5.5e-03 0.23
5 4.7e-01 1.0e-01 2.6e-01 -9.69e-01 6.941121688e+03 7.530801279e+03 1.5e-03 0.25
6 2.1e-01 4.6e-02 1.6e-01 -8.26e-01 1.592851972e+04 1.695003517e+04 7.0e-04 0.27
7 1.1e-01 2.5e-02 1.1e-01 -7.48e-01 2.865868558e+04 3.039795088e+04 3.7e-04 0.27
8 6.6e-02 1.4e-02 4.7e-02 -1.84e-01 4.094442197e+04 4.189788013e+04 2.2e-04 0.28
9 2.7e-02 5.9e-03 2.7e-02 -4.05e-01 6.644786733e+04 6.829513244e+04 8.9e-05 0.28
10 1.1e-02 2.4e-03 6.2e-03 6.30e-01 8.433128292e+04 8.491538249e+04 3.6e-05 0.28
11 6.4e-03 1.4e-03 3.1e-03 6.98e-01 8.954098631e+04 8.999380411e+04 2.1e-05 0.30
12 2.0e-03 4.4e-04 5.5e-04 9.71e-01 9.732338038e+04 9.746639681e+04 6.6e-06 0.30
13 1.0e-03 2.3e-04 2.5e-04 8.83e-01 9.841501124e+04 9.852323822e+04 3.5e-06 0.31
14 2.4e-04 5.4e-05 2.6e-05 1.16e+00 1.000163434e+05 1.000369433e+05 8.1e-07 0.31
15 9.8e-05 2.1e-05 7.6e-06 9.56e-01 1.001887509e+05 1.001998658e+05 3.2e-07 0.33
16 1.4e-05 3.2e-06 3.2e-07 1.21e+00 1.003288108e+05 1.003297199e+05 4.8e-08 0.33
17 2.8e-06 6.1e-07 2.5e-08 1.13e+00 1.003405834e+05 1.003407263e+05 9.3e-09 0.34
18 4.6e-09 1.6e-07 1.1e-10 1.00e+00 1.003430997e+05 1.003431001e+05 1.5e-10 0.34
19 4.4e-09 1.6e-07 9.1e-11 1.00e+00 1.003430962e+05 1.003430966e+05 1.5e-10 0.36
20 3.3e-09 1.2e-07 5.0e-11 1.00e+00 1.003430690e+05 1.003430692e+05 1.1e-10 0.36
21 2.9e-09 1.0e-07 4.4e-11 1.00e+00 1.003430588e+05 1.003430590e+05 9.8e-11 0.38
22 2.9e-09 1.0e-07 3.7e-11 1.00e+00 1.003430577e+05 1.003430579e+05 9.6e-11 0.39
23 2.7e-09 9.4e-08 3.3e-11 1.00e+00 1.003430533e+05 1.003430535e+05 9.0e-11 0.39
24 1.4e-09 6.0e-08 1.1e-11 1.00e+00 1.003430205e+05 1.003430206e+05 4.6e-11 0.39
25 1.3e-09 6.3e-08 5.9e-12 1.00e+00 1.003430195e+05 1.003430196e+05 4.4e-11 0.41
26 1.2e-09 6.6e-08 2.2e-12 1.00e+00 1.003430175e+05 1.003430176e+05 4.1e-11 0.42
27 1.2e-09 6.6e-08 2.2e-12 1.00e+00 1.003430175e+05 1.003430176e+05 4.1e-11 0.42
28 1.2e-09 6.8e-08 7.5e-12 1.00e+00 1.003430156e+05 1.003430157e+05 3.9e-11 0.44
29 1.1e-09 7.0e-08 4.0e-12 1.00e+00 1.003430152e+05 1.003430152e+05 3.8e-11 0.44
30 1.1e-09 7.8e-08 8.1e-12 1.00e+00 1.003430134e+05 1.003430135e+05 3.6e-11 0.45
31 1.1e-09 7.5e-08 4.3e-12 1.00e+00 1.003430132e+05 1.003430133e+05 3.6e-11 0.45
32 9.9e-10 7.8e-08 1.6e-12 1.00e+00 1.003430116e+05 1.003430117e+05 3.3e-11 0.45
33 9.9e-10 7.8e-08 1.6e-12 1.00e+00 1.003430116e+05 1.003430117e+05 3.3e-11 0.47
34 9.9e-10 7.9e-08 5.1e-12 1.00e+00 1.003430116e+05 1.003430117e+05 3.3e-11 0.47
35 5.0e-10 1.3e-07 3.4e-12 1.00e+00 1.003429995e+05 1.003429995e+05 1.7e-11 0.48
Optimizer terminated. Time: 0.56
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: 1.0034299948e+05 nrm: 2e+05 Viol. con: 1e-03 var: 0e+00 barvar: 0e+00 cones: 0e+00
Dual. obj: 1.0034299952e+05 nrm: 1e+05 Viol. con: 0e+00 var: 9e-10 barvar: 2e-09 cones: 4e-14
Optimizer summary
Optimizer - time: 0.56
Interior-point - iterations : 35 time: 0.48
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
Status: Solved
Optimal value (cvx_optval): -100343
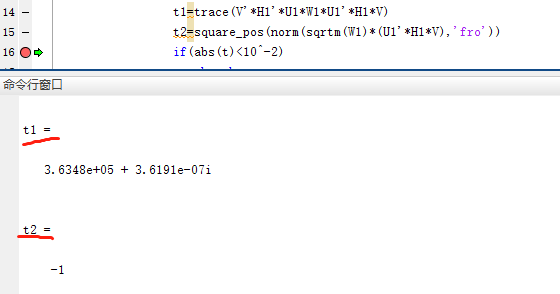
t1 =
9.169133569916600e+04 + 4.652019924833439e-08i
t2 =
9.169133569916851e+04
Calling Mosek 9.2.20: 167 variables, 31 equality constraints
For improved efficiency, Mosek is solving the dual problem.
MOSEK Version 9.2.21 (Build date: 2020-9-1 11:11:27)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 31
Cones : 6
Scalar variables : 67
Matrix variables : 2
Integer variables : 0
Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 2
Eliminator terminated.
Eliminator - tries : 1 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.03
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 31
Cones : 6
Scalar variables : 67
Matrix variables : 2
Integer variables : 0
Optimizer - threads : 8
Optimizer - solved problem : the primal
Optimizer - Constraints : 19
Optimizer - Cones : 6
Optimizer - Scalar variables : 57 conic : 56
Optimizer - Semi-definite variables: 2 scalarized : 172
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 184 after factor : 190
Factor - dense dim. : 0 flops : 6.47e+04
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 3.0e+02 8.9e+01 7.0e+00 0.00e+00 5.000421364e+00 -1.000000000e+00 1.0e+00 0.06
1 1.4e+02 4.1e+01 4.8e+00 -1.00e+00 -3.521003872e+01 -4.005120730e+01 4.6e-01 0.22
2 3.2e+01 9.3e+00 2.3e+00 -1.00e+00 -1.757025799e+02 -1.730886308e+02 1.0e-01 0.25
3 6.7e+00 2.0e+00 1.1e+00 -1.01e+00 -3.017449348e+02 -2.626666733e+02 2.2e-02 0.25
4 1.5e+00 4.5e-01 5.1e-01 -1.01e+00 8.368250793e+02 1.033324386e+03 5.1e-03 0.25
5 4.3e-01 1.3e-01 2.6e-01 -9.83e-01 6.885029031e+03 7.550701921e+03 1.4e-03 0.27
6 2.3e-01 6.9e-02 1.7e-01 -8.24e-01 1.391737450e+04 1.490777331e+04 7.7e-04 0.27
7 1.2e-01 3.5e-02 1.2e-01 -7.52e-01 2.760611168e+04 2.938128943e+04 4.0e-04 0.28
8 6.9e-02 2.0e-02 4.9e-02 -2.69e-01 4.033407789e+04 4.127126859e+04 2.3e-04 0.28
9 2.6e-02 7.6e-03 2.5e-02 -3.48e-01 6.821331993e+04 6.997707239e+04 8.6e-05 0.30
10 1.1e-02 3.2e-03 6.2e-03 6.88e-01 8.528679009e+04 8.588501652e+04 3.6e-05 0.30
11 6.4e-03 1.9e-03 3.3e-03 7.01e-01 8.968943913e+04 9.017419664e+04 2.1e-05 0.30
12 1.8e-03 5.4e-04 5.0e-04 9.78e-01 9.760694871e+04 9.774325038e+04 6.1e-06 0.31
13 8.8e-04 2.6e-04 2.0e-04 8.98e-01 9.874246113e+04 9.883730651e+04 2.9e-06 0.31
14 2.1e-04 6.3e-05 2.1e-05 1.16e+00 1.000578643e+05 1.000759994e+05 7.1e-07 0.33
15 8.7e-05 2.6e-05 6.4e-06 9.50e-01 1.002058632e+05 1.002157431e+05 2.9e-07 0.34
16 1.3e-05 4.0e-06 2.8e-07 1.23e+00 1.003295562e+05 1.003303774e+05 4.4e-08 0.34
17 1.8e-06 1.6e-06 1.4e-08 9.95e-01 1.003424898e+05 1.003426015e+05 6.6e-09 0.34
18 6.2e-09 8.7e-08 1.5e-10 1.00e+00 1.003430495e+05 1.003430499e+05 8.7e-11 0.36
19 5.8e-09 8.1e-08 6.9e-11 1.00e+00 1.003430456e+05 1.003430460e+05 8.2e-11 0.36
20 3.0e-09 8.4e-08 6.9e-12 1.00e+00 1.003430166e+05 1.003430168e+05 4.1e-11 0.38
21 2.9e-09 8.2e-08 1.1e-11 1.00e+00 1.003430165e+05 1.003430167e+05 4.1e-11 0.38
22 2.2e-09 1.2e-07 1.0e-11 1.00e+00 1.003430092e+05 1.003430094e+05 3.1e-11 0.39
23 2.2e-09 1.2e-07 1.0e-11 1.00e+00 1.003430092e+05 1.003430094e+05 3.1e-11 0.39
24 2.1e-09 1.2e-07 5.9e-12 1.00e+00 1.003430085e+05 1.003430087e+05 3.0e-11 0.41
25 1.6e-09 1.6e-07 7.5e-12 1.00e+00 1.003430032e+05 1.003430033e+05 2.2e-11 0.41
26 8.1e-10 2.5e-07 3.0e-12 1.00e+00 1.003429952e+05 1.003429953e+05 1.1e-11 0.42
Optimizer terminated. Time: 0.48
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: 1.0034299520e+05 nrm: 2e+05 Viol. con: 2e-03 var: 0e+00 barvar: 0e+00 cones: 0e+00
Dual. obj: 1.0034299525e+05 nrm: 1e+05 Viol. con: 0e+00 var: 1e-09 barvar: 3e-09 cones: 0e+00
Optimizer summary
Optimizer - time: 0.48
Interior-point - iterations : 26 time: 0.42
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
Status: Solved
Optimal value (cvx_optval): -100343
t1 =
9.169128964726381e+04 + 4.651565177482553e-08i
t2 =
9.169128964726634e+04
Show your code and the results all at once. I have no idea what is going on when you show two different windows, and perhaps, neither do you.
Too strange,dont konw how to deal next step.
Following is the cvx output messeage:
Calling Mosek 8.0.0.60: 167 variables, 31 equality constraints
For improved efficiency, Mosek is solving the dual problem.
MOSEK Version 8.0.0.60 (Build date: 2017-3-1 13:09:33)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 31
Cones : 6
Scalar variables : 67
Matrix variables : 2
Integer variables : 0
Optimizer started.
Conic interior-point optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 2
Eliminator terminated.
Eliminator - tries : 1 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.01
Optimizer - threads : 6
Optimizer - solved problem : the primal
Optimizer - Constraints : 19
Optimizer - Cones : 6
Optimizer - Scalar variables : 57 conic : 56
Optimizer - Semi-definite variables: 2 scalarized : 172
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 184 after factor : 190
Factor - dense dim. : 0 flops : 6.47e+004
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 4.0e+000 4.1e+003 1.0e+000 0.00e+000 6.400082949e+002 0.000000000e+000 1.0e+000 0.05
1 1.6e+000 1.7e+003 2.7e-001 -1.00e+000 -2.376025917e+004 -1.996351657e+002 4.0e-001 0.16
2 3.8e-001 3.9e+002 3.0e-002 -9.99e-001 -1.565681401e+005 -1.557348051e+003 9.5e-002 0.16
3 5.7e-002 5.8e+001 1.8e-003 -9.95e-001 -1.120029907e+006 -1.339634576e+004 1.4e-002 0.17
4 1.2e-002 1.3e+001 1.9e-004 -9.65e-001 -4.762713122e+006 -6.469740899e+004 3.1e-003 0.17
5 2.7e-003 2.8e+000 2.4e-005 -8.36e-001 -1.426353304e+007 -2.362499226e+005 6.7e-004 0.19
6 5.3e-004 5.5e-001 6.4e-006 -1.84e-001 -7.961201621e+006 -3.747400108e+005 1.3e-004 0.20
7 1.7e-004 1.8e-001 1.1e-005 1.36e+000 -4.986274873e+005 -2.319884747e+005 4.3e-005 0.20
8 8.3e-005 8.5e-002 1.3e-005 3.40e+000 -5.514590164e+004 -6.513286683e+003 2.1e-005 0.22
9 4.4e-005 4.5e-002 1.0e-005 2.26e+000 1.925479118e+004 3.944779616e+004 1.1e-005 0.23
10 1.9e-005 2.0e-002 7.3e-006 1.59e+000 3.615021470e+004 4.381128752e+004 4.8e-006 0.23
11 7.9e-006 8.1e-003 5.4e-006 1.42e+000 4.661034278e+004 4.895717167e+004 2.0e-006 0.25
12 5.5e-006 5.6e-003 4.0e-006 9.23e-001 4.691438907e+004 4.897774644e+004 1.4e-006 0.25
13 1.2e-006 1.2e-003 3.0e-006 1.29e+000 5.072978145e+004 5.091674736e+004 3.0e-007 0.27
14 5.1e-007 5.2e-004 1.6e-006 9.80e-001 5.093321918e+004 5.104134693e+004 1.3e-007 0.28
15 1.2e-007 1.2e-004 1.0e-006 1.22e+000 5.124681170e+004 5.126256213e+004 3.0e-008 0.28
16 5.0e-008 5.1e-005 5.8e-007 9.33e-001 5.126855119e+004 5.127651015e+004 1.2e-008 0.28
17 1.4e-008 1.5e-005 3.3e-007 1.18e+000 5.128899916e+004 5.129107109e+004 3.5e-009 0.30
18 5.9e-009 6.1e-006 1.3e-007 5.51e-001 5.128707337e+004 5.128921049e+004 1.5e-009 0.31
19 3.2e-009 2.1e-006 2.8e-008 -5.41e-001 5.127644215e+004 5.128226048e+004 5.0e-010 0.31
20 2.2e-009 8.9e-007 1.0e-008 -4.27e-001 5.123020413e+004 5.123806012e+004 2.1e-010 0.33
21 1.4e-009 4.1e-007 4.6e-009 -2.83e-001 5.115758279e+004 5.116588873e+004 9.8e-011 0.33
22 5.6e-010 1.9e-007 2.8e-009 2.91e-001 5.106152839e+004 5.106624913e+004 4.6e-011 0.34
23 2.9e-010 9.6e-008 1.4e-009 1.02e-001 5.099708474e+004 5.100183648e+004 2.3e-011 0.34
24 5.1e-011 1.7e-008 5.5e-010 7.46e-001 5.089299857e+004 5.089401089e+004 4.1e-012 0.36
25 6.5e-012 2.2e-009 1.8e-010 8.47e-001 5.086327638e+004 5.086343903e+004 5.3e-013 0.38
26 1.2e-011 1.1e-009 1.3e-010 9.77e-001 5.086090488e+004 5.086099016e+004 2.7e-013 0.38
27 1.4e-011 1.1e-009 1.3e-010 1.00e+000 5.086089990e+004 5.086098503e+004 2.7e-013 0.39
28 1.4e-011 1.1e-009 1.3e-010 1.00e+000 5.086089866e+004 5.086098375e+004 2.7e-013 0.41
29 1.4e-011 1.1e-009 1.3e-010 1.00e+000 5.086089835e+004 5.086098343e+004 2.7e-013 0.41
30 1.4e-011 1.1e-009 1.3e-010 1.00e+000 5.086089804e+004 5.086098311e+004 2.7e-013 0.42
31 1.4e-011 1.1e-009 1.3e-010 1.00e+000 5.086089773e+004 5.086098279e+004 2.7e-013 0.42
32 6.8e-012 1.1e-009 1.3e-010 9.96e-001 5.086088784e+004 5.086097257e+004 2.7e-013 0.44
33 1.0e-011 1.1e-009 1.3e-010 1.00e+000 5.086080877e+004 5.086089092e+004 2.6e-013 0.44
34 1.4e-011 1.1e-009 1.3e-010 1.00e+000 5.086079918e+004 5.086088102e+004 2.6e-013 0.45
35 1.3e-011 1.1e-009 1.3e-010 1.00e+000 5.086079858e+004 5.086088040e+004 2.6e-013 0.45
36 1.4e-011 1.1e-009 1.3e-010 1.00e+000 5.086079798e+004 5.086087978e+004 2.6e-013 0.47
37 1.4e-011 1.1e-009 1.3e-010 1.00e+000 5.086079679e+004 5.086087855e+004 2.6e-013 0.47
38 1.4e-011 1.1e-009 1.3e-010 1.00e+000 5.086079664e+004 5.086087840e+004 2.6e-013 0.48
39 1.4e-011 1.1e-009 1.3e-010 1.00e+000 5.086079634e+004 5.086087809e+004 2.6e-013 0.48
40 1.4e-011 1.1e-009 1.3e-010 1.00e+000 5.086079619e+004 5.086087793e+004 2.6e-013 0.50
41 1.4e-011 1.1e-009 1.3e-010 1.00e+000 5.086079560e+004 5.086087732e+004 2.6e-013 0.52
42 1.4e-011 1.1e-009 1.3e-010 1.00e+000 5.086079500e+004 5.086087670e+004 2.6e-013 0.52
43 1.4e-011 1.1e-009 1.3e-010 1.00e+000 5.086079500e+004 5.086087670e+004 2.6e-013 0.52
Interior-point optimizer terminated. Time: 0.53.
Optimizer terminated. Time: 0.58
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : NEAR_OPTIMAL
Primal. obj: 5.0860795001e+004 nrm: 4e+007 Viol. con: 1e-004 var: 6e-003 barvar: 0e+000 cones: 0e+000
Dual. obj: 5.0860876703e+004 nrm: 6e+004 Viol. con: 0e+000 var: 4e-004 barvar: 2e-007 cones: 0e+000
Optimizer summary
Optimizer - time: 0.58
Interior-point - iterations : 44 time: 0.53
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
Mosek error: MSK_RES_TRM_STALL ()
Status: Inaccurate/Solved
Optimal value (cvx_optval): -50860.9
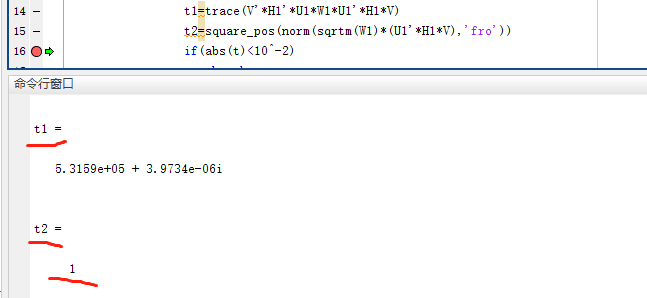
t1 =
4.4079e+04 - 8.1318e-10i
t2 =
1The output of t1 and t2 doesn’t match what you showed earlier.
Mosek did not solve to the desired tolerance. Nevertheless, I don’t see how that would result in the t2 value you show. Perhaps square_pos got corrupted.
Given your use of Mosek 8.0.0.60, it seems likely you are using CVX 2.1. I recommend you delete all CVX directories from your MATLAB path, then start a new MATLAB session, and install CVX 2.2. You will then have Mosek 9.1.something. If you download Mosek 9.2.x from the Mosek site, then choose that version of Mosek, which you can see from cvx_solver. Or before installing CVX 2.2, rename the mosek directory under the CVX directory to something else - then CVX won’t find it, and you will have only the version of Mosek you downloaded, so can just specify cvx_solver mosek, rather than cvx_solver Mosek_2 or whatever.
OK, thank you Mark for you patience and help. I’ll have a try.