how does sdpt3 convert regularized problem into constrained problem for a given lambda ,
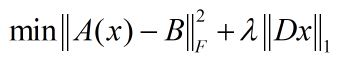
SDPT3 is not doing such a conversion. If you use CVX, it will convert this problem into an SOCP which it passes to the solver.http://web.stanford.edu/~boyd/papers/pdf/mcg_thesis.pdf
I am presuming that \lambda is provided as input data (a numerical value when you input this to CVX,otherwise it won;t even be accepted by CVX. It is up to you to determine what value of \lambda to use, or perhaps use Cross Validation to choose it by solving a series of CVX problems each having a different value of |lambda.
ok then , how does cvx convert this , i’m more interested in the theory thing
i mean how can we remove the second term and replace it with a constraint , for a specific lambda so that the solution of the two problems is exactly the same
Even the first term is moved to the constraints via epigraph formulation.
So something like this if the frobenius norm were not squared
variables t1 t2
minimize(t1 + t2)
norm(A*x-B),'fro) <= t1
lambda*norm(D*x),1) <= t2
with some other ,modification to handle the squaring of the frobenius norm.
There is some \lambda value (or range of values) to use as the right-hand side of a <= constraint such that it will have the same solution as some other value of \lambda in the unconstrained problem. You can find this value by solving them. You won’t know in advance. If you have further questions on this, I suggest you ask at https://math.stackexchange.com/ or https://or.stackexchange.com/ .
are u treating x as being known ? , one last question , is there a cross validation function in cvx , or i must do that manually for a grid of lambda values
I have been presuming that x is the unknown, i…e CVX (optimization) variable, within a given CVX problem instance.
CVX does not have a cross validation function. Take a look at http://cvxr.com/cvx/doc/quickstart.html#an-optimal-trade-off-curve for a related do it yourself calculation.
thanks sir , u are extremely helpful and kind
If you have questions about cross validation, the best place to ask is https://stats.stackexchange.com/ I recommend you search “cross validation” on the site. You will learn a lot. Then ask a question if you still need help.
If you really want to learn about cross validation, read https://web.stanford.edu/~hastie/Papers/ESLII.pdf .section 7.10.
i understand that cvx solves this after converting it to sdp form , how can the L1 penalty be converted to sdp form inequality ?
L1 penalty can be handled via linear constraints (which are a special case of second order cone constraints).
CVX doesn’t convert anything to SDP form unless it has to. It actually converts those SDP constraints which it knows can be formulated as SOC constraints (all 2 by 2 SDP constraints plus certain higher dimension instances) into SOC constraints, because those are more efficiently solved by the solvers. All linear and SOC constraints can be formulated as SDP constraints, but that is not an efficient way to solve them, and CVX does not provide them as SDP constraints to the solver it calls.
If you really want to improve your understanding of all this, invest the intellectual shoe leather to read and work the Exercises in “Convex Optimization”, Boyd and Vandenberghe https://web.stanford.edu/~boyd/cvxbook/ at least through chapter 7.
what if we transform the problem like this to get rid of L1 norm
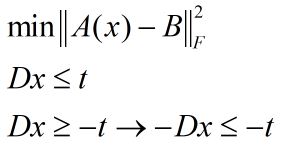
then what do u suggest next step to be , t is an unknown vector ,
no longer a scalar like in your previous suggestion , how to go ahead with this , the two inequality constraints to account for L1 norm
So you have an n element vector.t. See https://math.stackexchange.com/questions/1639716/how-can-l-1-norm-minimization-with-linear-equality-constraints-basis-pu .
Anyhow, you are spared these under the hood complications if you use CVX, which directly lets you use the one norm in an objective or constraint, as long as it is used in a convex fashion (in accordance with DCP rules).
actually i want to solve the problem using cvx_opt but it is provided only in python and does not provide an L1 regularization so i somehow have to deal with it seperately by transform it to constraint thats why!
If you want to use Python, use CVXPY instead of CVXOPT (actually CVXPY can call CVXOPT solvers, among others). CVXPY has the same ability to handle norms as does CVX, so you don’t need to convert norms to other representations. CVXPY (or CVX) does what it needs to do for you, and saves you the pain and error propensity of converting the problem to a form accepted by the solver.
If you need help with CVXPY, ask at https://groups.google.com/forum/#!forum/cvxpy .
there is a specialized fast functions that handles nuclear norm problems by exploiting problem structures designed by vandenberghe , they are coded in python and uses cvx_opt routines but unfortunately only quadratic regularization with linear and sdp LMI , so i thought lets transform L1 regularization term to LMI and call that function 