How can I express this term into CVX form?

1

Dear anyone,

The term is given as following:

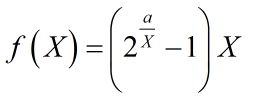
image
where a is a positive constant, and each element of matrix X is positive variable, this expression is convex. How can I express this term into CVX form?
Is it right written like this way:

  • (2.^(a.*inv_pos(X))-1).*X

Thanks in advance!

2

I presume X is a scalar, not a matrix. If so, follow my suggestions in Convert problem to cvx .

If X is a matrix, you need to further clarify.

3

Dear Mark,
Thanks for your answer. In my simulation, X is indeed a matrix. I follow your suggestion, however, I get a bad result, the status shows unbounded.

function [ a,objective2 ] = OptimalResourceAllocation( L_mu,h_M2U )
global SNR B Epsilon2 Epsilon1 K N delta P_static
cvx_begin
      variables a(N,K) z(N,K) 
      expression  E_mu(N,K)
      for k=1:K
          for n=1:N
              E_mu(n,k)=(1./Epsilon1*(z(n,k)-a(n,k))*h_M2U(n,k)/SNR+Epsilon2*a(n,k)+P_static)*delta;
          end
      end
      minimize sum(sum(E_mu))
      subject to 
      for k=1:K
          for n=1:N
             {L_mu(n,k)./(delta*B)*log(2),a(N,K),z(N,K)} == exponential(1);
          end
      end
      for n=1:N
          sum(a(n,:))<=1;
      end
      a>=0.0001;
cvx_end
objective2=sum(sum(E_mu));
end

%%%%%%%%%%%%%%%
Successive approximation method to be employed.
Mosek will be called several times to refine the solution.
Original size: 2332 variables, 892 equality constraints
320 exponentials add 2560 variables, 1600 equality constraints
-----------------------------------------------------------------
Cones | Errors |
Mov/Act | Centering Exp cone Poly cone | Status
--------±--------------------------------±--------
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Unbounded
-----------------------------------------------------------------
Status: Unbounded
Optimal value (cvx_optval): -Inf

a1 =

   sparse matrix : 40×4

why this result incurs?

4

Have you tried to simplify things to where you can check out certain parts of your problem, and then build up to the problem you really want to solve?

Can you provide a complete (and if possible, small) reproducible example, with all input values provided?

I have no idea what your program does or what you want it to do, other than that it involves exponential cone constraints.