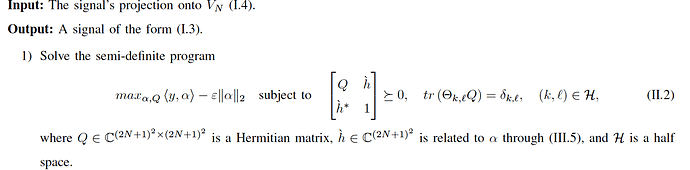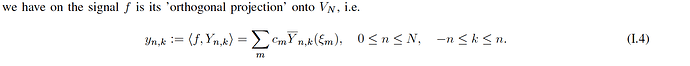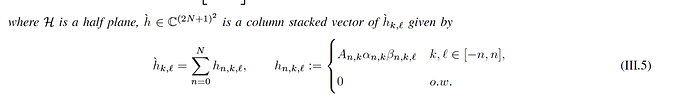Hi everyone!
I am new in CVX.
Could you, please, help me (or give an advice) what I need to change to make the following problem work.
Namely, I try to implement the following problem:
where
I have to versions of the code, but non of them seems to work and give correct result:
Version 1:
clear all
disp('Initialization...')
%number of samples
% true number of spikes nspikes = floor(N/19.2);
N=5;
theta_m=linspace(0.1,pi*0.9,3);
phi_m=linspace(0.1,2*pi*0.9,3); % second azimuth (0, 2*pi);
%number of spikes
nspikes= length(theta_m);
%coeffs
coeff= rand(nspikes,1);
% matrix of samples
YY=sammax(N, theta_m(:), phi_m(:));
y_mes=YY*coeff; % data vector
%%computing needed Legendre polinomials
P=cell_of_LegendreP(N);
%% for SPD coffeicients
Ank=@(n,k) sqrt(((2*n+1)/(4*pi))*factorial(n-k)/factorial(n+k));
% sqrt((2*n+1)/(4*pi)*factorial(n-abs(k))/factorial(n+abs(k)));
% Toepliz matrices
Q=@(M,j) diag(ones(M-abs(j),1),j);
disp('Sonving SDP...')
%% Solve SDP 1
cvx_solver SDPT3
cvx_precision high
cvx_begin sdp
%cvx_begin sdp
variable X((2*N+1)^2,(2*N+1)^2) hermitian;
variable c((N+1)^2) complex;
expressions K((2*N+1)^2) complex;
for k= -N:N
for l = -N:N
hlk=cvx(0);
for n= 0:N
hnlk=cvx(0);
% hnkl formular
I=-n:n;
if ismember(k,I)&&ismember(l,I)
p = P{n^2+1+n+k};
hnlk= c(n^2+1+n+k)*Ank(n,k)*p(n+1+l);
else
hnlk=0;
end
% hnkl formular
hlk= hlk+ hnlk;
end
K((N+k)*(2*N+1)+N+1+l)= hlk;
end
end
disp('First constraint...')
[ X, K; K', 1] >= 0;
% trace([ X, K; K', 1]) == 2;
trace(X) == 1;
% h == K;
for j = -2*N:2*N
for k = -2*N:2*N
if isinhalfspace1(j,k)
%clear th;
th = kron(Q(2*N+1,j),Q(2*N+1,k))';
th(:)'*X(:) == double( (j==0) & (k==0));
end
end
end
disp('Second constraint...')
maximize(real(c'*y_mes))
cvx_end
Version 2:
disp('Sonving SDP 2...')
%% Solve SDP
cvx_solver SDPT3
cvx_precision high
cvx_begin sdp
variable X((2*N+1)^2+1,(2*N+1)^2+1) hermitian
variable c((N+1)^2) complex
expressions K((2*N+1)^2) complex
dual variable R
R: X >= 0
% constraints
for k = -N:N
for l = -N:N
hlk = 0;
% hlk formular
for n = 0:N
hnlk = 0;
% hnkl formular
I=-n:n;
if ismember(k,I)&&ismember(l,I)
p = P{n^2+1+n+k};
hnlk = c(n^2+1+n+k)*Ank(n,k)*p(n+1+l);
end
hlk = hlk+ hnlk;
end
K((N+k)*(2*N+1)+N+1+l) = hlk;
end
end
disp('First constraint...')
trace(X) == 2;
X((2*N+1)^2+1,(2*N+1)^2+1) == 1;
X(1:(2*N+1)^2,(2*N+1)^2+1) == K;
% X((2*N+1)^2+1,1:(2*N+1)^2)' == K;%K(2:(2*N+1)^2+1) ;
disp('First constraints...')
MM=X(1:(2*N+1)^2,1:(2*N+1)^2);
for j = -2*N:2*N
for k = -2*N:2*N
if isinhalfspace1(j,k)
%clear th;
th = kron(Q(2*N+1,j),Q(2*N+1,k))';
th(:)'* MM(:) == double( (j==0) & (k==0));
end
end
end
disp('Second constraint...')
maximize(real(c'*y))
cvx_end
Moreover the algorithm fails when N increases, for example N=10.
I also have tried to use MOSEK as a solver, but any way it does not work.
P.S: here for sammax I use :
function YN =sammax(N,th,phi)
%n = floor((N+1)^2);
Y1= [];
th = th(:); %0:pi
phi = phi(:); %0:2*pi
for s = 0:N
for r = -s:s
Y1 = [Y1 harmonicY(s,r,th,phi)];% sphHarm(s,r,th,phi)];%
end
end
YN= Y1';
where harmonicY are spherical harmonics