Help: Illegal operation: {real affine} - {invalid}

1

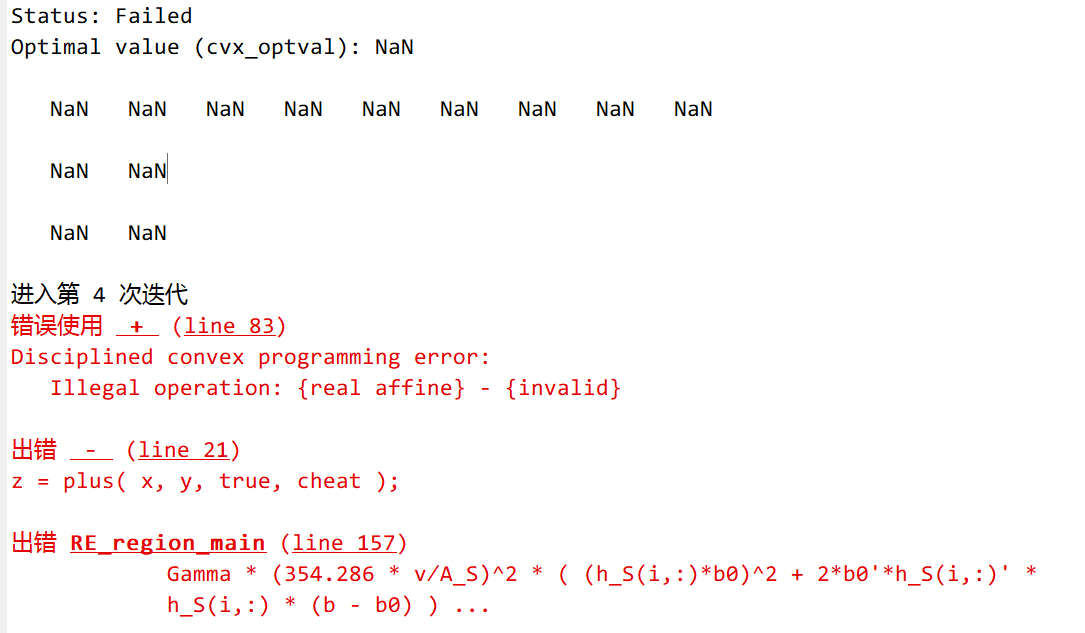
1616575743(1)
1616575743(1)1085×633 17.1 KB

Hello, a error occured when I run my code, my code is as follows, please help me. Thanks!

clc;
clear all;
A_P = 10^(-4);
A_S = 10^(-3);
half_angle = pi/3;
Psi_P = pi/3;
Psi_S = pi/3;
A = 2;
varepsilon = 1;
I_sc = 0.2;
U_oc = 5;
alpha_stc = 0.00175;
E_a = 0.4;
rho = 1;
eta = 0.75;
T_stc = 298;
E_stc = 1000;
T_a = 298;
sigma = -98.82;
xi = -log(2)/log(cos(half_angle));
T_P = 1;
T_S = 1;
N = 9;
K = 2;
LED_x = [4.9 4.9 4.9 5.0 5.0 5.0 5.1 5.1 5.1];
LED_y = [4.9 5.0 5.1 4.9 5.0 5.1 4.9 5.0 5.1];
LED_z = [3.0 3.0 3.0 3.0 3.0 3.0 3.0 3.0 3.0];
PD_x = [5.1 5.1];
PD_y = [6.0 4.0];
PD_z = [1.5 1.5];
Solar_x = [5.0 5.0];
Solar_y = [5.1 4.9];
Solar_z = [1.5 1.5];
tau = 0.9;
P_o = 30;
K_m = 683;
c_1 = 0.026;
J = 1.6;
c = 1/(J*c_1);
P_t = 53.8;
Q_t = 4.7164;
v = 1/320;
I_H = 12;
I_L = 0;
kesai = 10^(-3);

for i = 1:1:K
for j = 1:1:N
d_P(i,j) = sqrt( (LED_x(j) - PD_x(i))^2 + (LED_y(j) - PD_y(i))^2 + (LED_z(j) - PD_z(i))^2 );
phi_P(i,j) = acos( (LED_z(j) - PD_z(i)) / d_P(i,j) );
psi_P(i,j) = phi_P(i,j);
if psi_P(i,j) > Psi_P
g_P(i,j) = 0;
else
g_P(i,j) = (rho/sin(Psi_P))^2;
end
h_P(i,j) = ( A_P * (xi + 1) * cos(phi_P(i,j))^xi * cos(psi_P(i,j)) * g_P(i,j) * T_P ) / (2 * pi *d_P(i,j)^2);
end
H_P(:,:,i) = h_P(i,:)’ * h_P(i,:);
end

for i = 1:1:K
for j = 1:1:N
d_S(i,j) = sqrt( (LED_x(j) - Solar_x(i) )^2 + (LED_y(j) - Solar_y(i))^2 + (LED_z(j) - Solar_z(i))^2 );
phi_S(i,j) = acos( (LED_z(j) - Solar_z(i)) / d_S(i,j) );
psi_S(i,j) = phi_S(i,j);
if psi_S(i,j) > Psi_S
g_S(i,j) = 0;
else
g_S(i,j) = (rho/sin(Psi_S))^2;
end
h_S(i,j) = ( A_S * (xi + 1) * cos(phi_S(i,j))^xi * cos(psi_S(i,j)) * g_S(i,j) * T_S) / (2 * pi d_S(i,j)^2);
end
H_S(:,:,i) = h_S(i,:)’ * h_S(i,:);
end
Gamma = eta(I_sc+alpha_stc*(T_a-T_stc))/(c * E_stc);
I_s0 = I_sc/(exp(c * U_oc)-1);
lamda = I_sc / (E_stc * I_s0);
om = ones(N,1);
d_widehat = kron([varepsilon^(1/2),varepsilon^(1/2)]’,om);
%% kron
for i = 1:1:K
H_P_1(:,:,i) = kron(diag([5.4116,5.4116]),H_P(:,:,i));%（N * K,N * K）
G_S(:,:,i) = kron(diag([varepsilon,varepsilon]),H_S(:,:,i));%（N * K,N * K）
end

for i = 1:1:K
if i == 1
H_P_2(:,:,i) = kron(diag([0,varepsilon]),H_P(:,:,i));%（N * K,N * K）
else
H_P_2(:,:,i) = kron(diag([varepsilon,0]),H_P(:,:,i));%（N * K,N * K）
end
end

for i = 1:1:N
em = zeros(N,1);
em(i) = 1;
a_n(:,i) = kron([A,A]’ ,em);%a_n
end
b0 = [2.5 2.5 1.5 2.5 2.5 2.5 2.1 2.5 2.5]’;
x0 = [4.6 4.6]’ ;
y0 = [-18 -18]’ ;
k = 0;
while(1)
k = k + 1;
cvx_begin
cvx_solver sedumi
variable W(N * K,N * K) symmetric semidefinite; %
variable Miu(K,1) nonnegative;
variable b(N,1) nonnegative;
variable x(K,1) nonnegative;
variable y(K,1);
maximize(sum(Miu))
subject to
for i = 1:1:K
trace( W * H_P_1(:,:,i) ) - exp( x(i) + y(i) ) >= 2 * pi * 10^( sigma / 10) * 10^(-3) * ( 2^( 2 * Miu(i)) - 1 );
end
sum(b) == tau * P_o;
trace(W.*(d_widehat * d_widehat’ )) + pow_pos(norm(b,2),2) <= 10^( P_t / 10) * 10^(-3);

for i = 1:1:K
    10^( Q_t / 10) * 10^(-3) - Gamma * (354.286 * v/A_S)^2 * trace(W * G_S(:,:,i)) <= ...
        Gamma * (354.286 * v/A_S)^2 * ( (h_S(i,:)*b0)^2 + 2*b0'*h_S(i,:)' * h_S(i,:) * (b - b0) ) ...
        + 2*Gamma*354.286 * v/A_S*(27*v/A_S*h_S(i,:)*om + E_a)*( h_S(i,:) * b ) + Gamma*(27*v/A_S*h_S(i,:)*om+E_a)^2 ...
        + Gamma*(-rel_entr(1,lamda) - 1) * (v/A_S * (354.286*h_S(i,:)*b + 27*h_S(i,:)*om) + E_a);
end

for i = 1:1:N
     trace(W * a_n(:,i) * a_n(:,i)') <= b0(i)^2 + 2 * b0(i) * ( b(i) - b0(i) );
end

for i = 1:1:N
     trace(W * a_n(:,i) * a_n(:,i)') <= b0(i)^2 + 2 * b0(i) * ( b(i) - b0(i) ) - 2 * I_H * b(i) + I_H^2;
end

for i = 1:1:K
    exp(x0(i)) + exp(x0(i)) * (x(i) - x0(i)) >= pi * 2^(2 * Miu(i) + 1);
end
 
for i = 1:1:K
    exp(y0(i)) + exp(y0(i)) * (y(i) - y0(i)) >= trace(W * H_P_2(:,:,i));
end     

cvx_end

mu_st(k) = sum(Miu);
if k>1
    if abs( mu_st(k) - mu_st(k-1) ) / mu_st(k) <= kesai
        break;
    end
end
b0 = b;
for i = 1:1:K
    x0(i) = log(trace(pi * 2^(2 * Miu(i) + 1)));
    y0(i) = log(trace(W * H_P_2(:,:,i)));
end

end

2

One time through the outer loop, CVX failed, which resulted in CVX variables being NaN. These NaN variables were used the next time through the outer loop, which resulted in invalid.

Follow the advice at
CVXQUAD: How to use CVXQUAD's Pade Approximant instead of CVX's unreliable Successive Approximation for GP mode, log, exp, entr, rel_entr, kl_div, log_det, det_rootn, exponential cone. CVXQUAD's Quantum (Matrix) Entropy & Matrix Log related functions . Maybe CVX won’t fail. But it still might. Try to make the problem as well-scaled as you can. Using Successive Convex Approximation in a crude way, such as you have, often doesn’t work out. Given the semidefinite declaration, perhaps your original problem is actually a Nonlinear Semidefinite Programming problem, which is very difficult to solve - your best best on that might be using BMIBNB under YALMIP, which may or may not succeed.

4

Please show your complete code. using CXVQUAD. If your original code did not produce any Disciplined convex programming errors, then the modifications for CVXQUAD per the link I provided should not result in concave <= real affine.

6

This looks like a bug in CVXQUAD:

trace_mpower(W,1,A_n)
ans =
    cvx concave expression (scalar)

This is why the error occurs. That expression should be affine. I opened an issue trace_mpower(matrix,1) returns concave expression instead of affine at the CVXQUAD GitHub site.

There really is no point to using CVXQUAD’s trace_mpower with an exponent of 1. You can instead just use trace:

trace(A_n*W)
ans =
    cvx real affine expression (scalar)
8

Other than the mention of CVXQUAD my first post of this thread still applies.