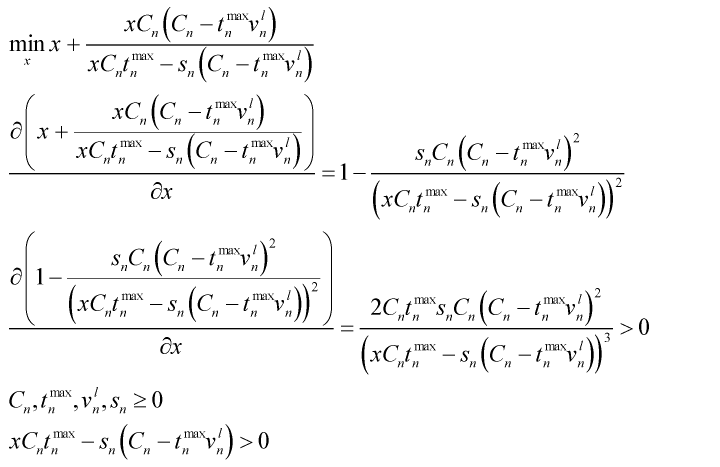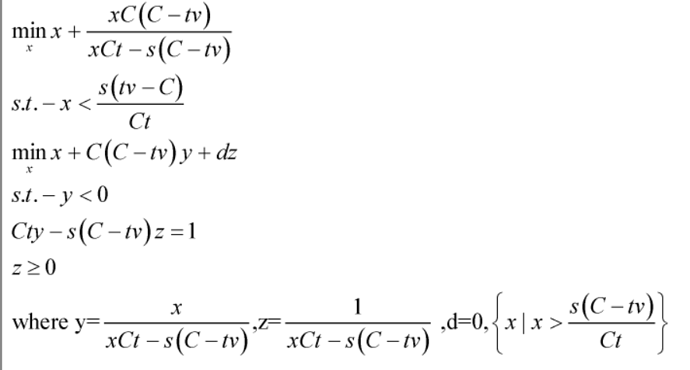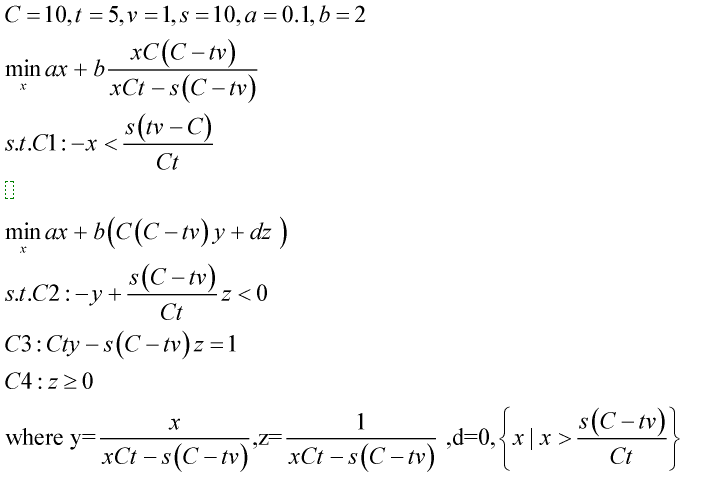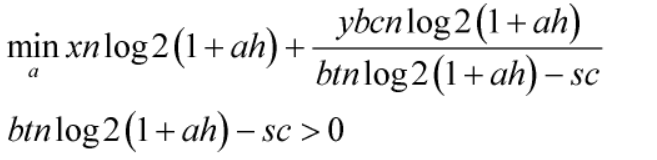
Regarding this type of objective function, how to use cvx to program effectively, I have a lot of problems in the compilation, here only a is variable, and the other parameters are constants.
You haven’t told us what any of the constants are. So I created a simplified version which I believe is a special case of your objective function.
f := log(1+a)+log(1+a)/(log(1+a)-1)
The 2nd derivative of f can be of either sign, depending on the value of a. Choosing a = 15, the constraint is satisfied and the 2nd derivative of f is negative, so the objective function is not convex on the entirety of the feasible set you have shown us, let alone on the entirety of its natural domain.
If there are specific values of the constants such that this is a convex optimization problem, you need to tell us what they are, and show us your convexity proof. However, if the objective function is convex on the feasible set, but not for the entirety of its natural domain, the prospects for being able to enter it in CVX would not be good.
First of all, thank you very much. According to your opinion, I modified my objective function, but there are still some problems in the implementation of CVX. I also gave a convex proof of the function, how can I effectively convert this objective function into feasible the cvx goal
Look at section 4.3.2 “Linear-fractional programming” of https://web.stanford.edu/~boyd/cvxbook/
If x is the only variable in your formula then have a look at https://docs.mosek.com/modeling-cookbook/cqo.html#rational-functions
Thank you very much. Based on your suggestions, after reading this part of the book, I transformed my question into the following form,like
After the next step, I can solve the problem I need using linear programming, but I read some information about the lower bound of a parameter, such as x> = 0 and x> 0, how to distinguish them during programming
Thank you very much for sharing, I learned a lot from here.But I am not very familiar with matlab, so the progress is slow, I am still looking at this knowledge
All inequalities in CVX and the solvers it calls are treated as non-strict, i.e., <= or >=. If you really need a strict inequality, you must incorporate a small positive number, small_number, into a non-strict inequality, such as x >= 1e-5, instead of x > 0.


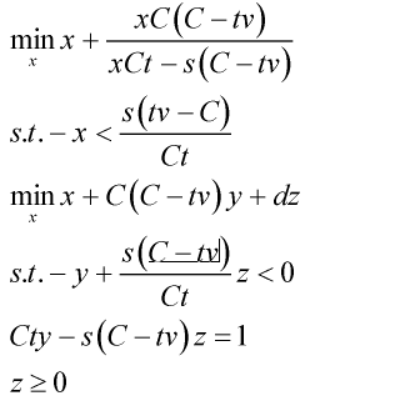
I finished writing, but the value of x that I expected was inconsistent with it, it should be a number greater than 0, if it is 0, the goal is meaningless
I have no idea what you’re doing. You showed us a problem with a scalar x, and you solved a problem with a 3 by 1 vector x. And you used linprog, not CVX.
Also, please copy and paste code, don’t use images. That allows readers to copy and paste your code in order to run it.
Because someone told me that using linear programming would be a better solution, but if I use cvx, how do I implement it? I do n’t know how to start with cvx
C=5; s=15;t=3; v=1; G=-1;
h=s*(tv-C)/(Ct)
c=[1 C*(C-tv) 0]
A=[0 -1 s(C-tv)/(Ct)]
b=[0]
Aeq=[0 Ct s(C-t*v)]
beq=[1]
vlb=[1e-5 1e-5 0]
vub=[]
[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)
This is the code I am currently programming, there may be some writing errors, which makes the results worse
Start by reading the CVX Users’ Guide. CVX can be used for Linear Programming problems. http://cvxr.com/cvx/doc/ Try models in the Users’ Guide, then modify them.
%***********************************************************************
% %Set common parameters***
clc;clear all;close all
C=10;s=0;t=5;v=1;
a=0.1;b=2;d=0;
i=1
for s=10:10:100
cvx_begin
variables x y z;
minimize a*x+b*(C*(C-t*v)*y+d*z)
subject to
z*s*(C-t*v)/(C*t)-y<0;
C*t*y-s*(C-t*v)*z==1;
z>0;
y>0;
% x>0;
x>s*(C-t*v)/(C*t);
cvx_end
opt_x(i)=x
opt_v(i)=C*(C-t*v)*y
opt_vn(i)=x*C*(C-t*v)/(x*C*t-s*(C-t*v))
q=a*x+b*C*(C-t*v)*y+d*z
co(i)=q
ee(i)=0.05*(C+s)/q
i=i+1;
end
figure(1),q=plot(10:10:100,co,‘b-d’);
figure(2),ee=plot(10:10:100,ee,‘b-d’);
This is my code, but the expected result deviates from my theory, because it can be seen that the opt_v item here has not even changed, and after I introduced the original calculation relationship, I found that the denominator item is 0. Is there something wrong with my programming
As I told you, strict inequalities are not honored as strict by CVX. Did you see the warning messages CVX provides when you use them?