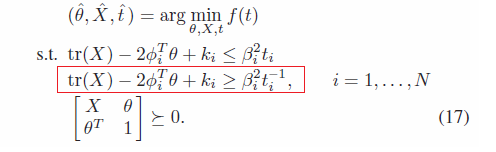Hello everybody, I am reproducing this paper http://www.bigdatalab.ac.cn/~wouyang/pubs/Received%20Signal%20Strength-Based%20Wireless%20Localization%20via%20Semidefinite%20Programming%20Noncooperative%20and%20Cooperative%20Schemes.pdf.
To be exact, I am implementing the eq. 17. 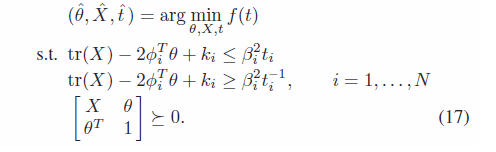 .
.
The first error is “Error using sym>tomupad (line 1251)
Unable to convert ‘cvx’ to ‘system’.” To avoid this error and see if the rest of the code works I set up X=eye(2) and I got another error: "Error using reshape
To RESHAPE the number of elements must not change.
Error in cvx/cat (line 88)
yb = reshape( yb, nz, psz );
Error in cvx/vertcat (line 6)
y = cat( 1, varargin{:} );".
Here, part of the code:
cvx_begin
variables theta(2) t(N); % theta= [x y] target loc. % N=number of anchors
X= thetatheta’; % X -> auxiliary variable
% X= eye(2);
minimize(norm(t, inf))
subject to
for i =1:N
trace(X) - 2phi(i,:)*theta +Ki(i) <= Bi_sqr(i)t(i);
[ trace(X) - 2phi(i,:)*theta +Ki(i), sqrt(Bi_sqr(i));
sqrt(Bi_sqr(i)), t(i)] >= 0;
[ X, theta;
theta’, 1 ]>= 0;
end
cvx_end
I am new with this tool, my apologies if my questions are so basic. Any help you can provide will be greatly appreciated.
 theta +Ki(i) >= Bi_sqr(i)(1/t(i));
theta +Ki(i) >= Bi_sqr(i)(1/t(i));