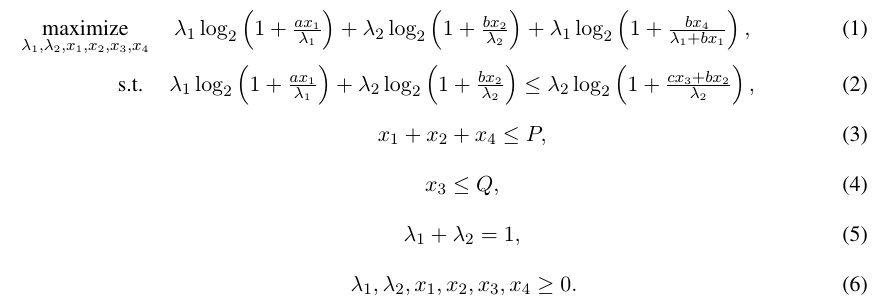The pre-condition is a>b, so I can prove that the objective function is concave. The challenge is how to process constraint (1), since both sides of (1) are concave. I feel so close to the right answer, but still can not find a good way to it. Does anyone have a clue? Many thanks!
Nothing at
seems useful.
Is there a good reason x_3=Q is not optimal.
Thank you, Erling!
If constraint (1) is inactive, we can always decrease x_{3} until (1) is avtive. If constraint (3) is inactive, we can always increase x_{4} until (3) is active. So we have at most two equations. Those are what I can think of.