Hi all,
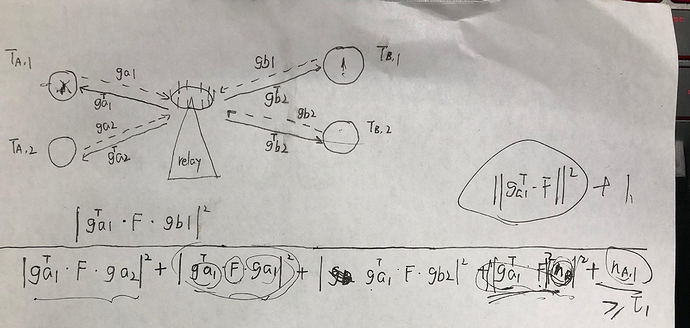
I encountered a problem when I use CVX. For a multi-pair two-way relaying system, there are 2 pairs of users and 2 antennas in the relay. My optimization is to make SINR larger than several specific values (SINR constraints). My optimization formulation is here:
My code is here:
clc
clear all
M=4;
N=2;
SINR_constraint_dB=(10:5:40);
MonteCarlo_number=2;
Y=[];
for i=1:MonteCarlo_number
channelA=sqrt(1/2)(randn(4,2)+1jrandn(4,2));
channelB=sqrt(1/2)(randn(4,2)+1jrandn(4,2));
ga1=channelA(:,1);
ga2=channelA(:,2);
gb1=channelB(:,1);
gb2=channelB(:,2);
n_r=sqrt(1/2)(randn(4,1)+1jrandn(4,1));
n_A=1;
n_B=1;
x=[];
y=[];
for SINR_constraint_dB=10:5:40
SINR_constraint=10.^(SINR_constraint_dB/10);
cvx_solver sedumi
cvx_begin
variable F(4,4) semidefinite
a=pow_pos(norm(F,‘fro’),2);
minimize a;
subject to
pow_pos(abs(trace(F*(gb1ga1.’))),2)>=SINR_constraint(pow_pos(abs(trace(F*(ga1ga1.’))),2)+pow_pos(abs(trace(F(ga2ga1.’))),2)+pow_pos(abs(trace(F(gb2ga1.’))),2)+pow_pos((norm(ga1.'F)),2)+(abs(n_A(1)))^2);
pow_pos(abs(trace(F(gb2ga2.’))),2)>=SINR_constraint*(pow_pos(abs(trace(F*(ga1ga2.’))),2)+pos_pos(abs(trace(F(ga2ga2.’))),2)+pow_pos(abs(trace(F(gb1*ga2.’))),2)+pow_pos((norm(ga2.’*F)),2)+(abs(n_A(2)))^2);
cvx_end
x=[x,SINR_constraint_dB];
y=[y,a]
end
Y=[Y;y];
end
average_transmit_power=sum(Y)/MonteCarlo_number;
plot(x,average_transmit_power,’-ok’);
xlabel(‘SINR constraint (dB)’);
ylabel(‘Average Transmit Power’);
legend(‘conventional’);
grid on
But there is a error:
Error using cvxprob/newcnstr (line 192)
Disciplined convex programming error:
Invalid constraint: {convex} >= {convex}
Error in >= (line 21)
b = newcnstr( evalin( ‘caller’, ‘cvx_problem’, ‘[]’ ), x, y, ‘>=’ );
Error in relay4antennas2pair (line 29)
pow_pos(abs(trace(F*(gb1ga1.’))),2)>=SINR_constraint(pow_pos(abs(trace(F*(ga1ga1.’))),2)+pow_pos(abs(trace(F(ga2ga1.’))),2)+pow_pos(abs(trace(F(gb2*ga1.’))),2)+pow_pos((norm(ga1.’*F)),2)+(abs(n_A(1)))^2);
How can I solve this?