Constraints with matrices

1

Hello,

Example:

cvx_begin
variable Sigma2(n,n) symmetric
maximize ( w'*Sigma2*w )
subject to
Sigma2 == semidefinite(n); % Sigma2 is positive semidefinite
Sigma2(1,1) == 1
Sigma2(1,2) >= 0
Sigma2(1,3) >= 0
Sigma2(2,1) >= 0
Sigma2(2,2) == 1
Sigma2(2,3) <= 0
Sigma2(2,4) <= 0
Sigma2(3,1) >= 0
Sigma2(3,2) <= 0
Sigma2(3,3) == 1
Sigma2(3,4) >= 0
Sigma2(4,2) <= 0
Sigma2(4,3) >= 0
Sigma2(4,4) == 1
cvx_end

Can express these constraints with two matrices L and U instead of by elements? These are the constraints:

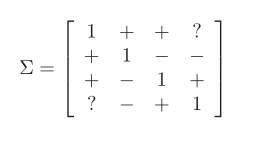
image

I tried:

U =

     1   Inf   Inf   Inf
   Inf     1     0     0
   Inf     0     1   Inf
   Inf     0   Inf     1

>> L

L =

     1     0     0  -Inf
     0     1  -Inf  -Inf
     0  -Inf     1     0
  -Inf  -Inf     0     1

But this constraint is not convex.

Error using cvxprob/newcnstr (line 192)
Disciplined convex programming error:
Invalid constraint: {real affine} >= {invalid}

Error in >= (line 21)
b = newcnstr( evalin( ‘caller’, ‘cvx_problem’, ‘[]’ ), x, y, ‘>=’ );

Error in cvx_proba2 (line 6)
Sigma2 >= L;

cvx_begin
variable Sigma2(n,n) symmetric
maximize ( w'*Sigma2*w )
subject to
Sigma2 == semidefinite(n); % Sigma2 is positive semidefinite
Sigma2 >= L
Sigma2 <= U
cvx_end

Thank you.

2

It’s not that the constraint is convex. Rather, although undocumented, it appears that CVX does not allow -Inf or Inf for constraint bounds, and declares -Inf or Inf to be invalid in such usage… This is unlike many optimizers under MATLAB, to include linprog, as shown in the example at http://cvxr.com/cvx/doc/quickstart.html#other-norms-and-functions

I don’t think it is numerically advisable to provide an explicit large magnitude bound, such as 1e20, in lieu of infinity, because that may be stressing to the solver. So I think you are best off with sticking with your first approach, or similar.

1 Like