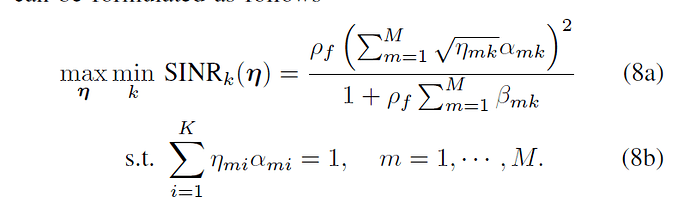Dear Stone,thanks to your reply.
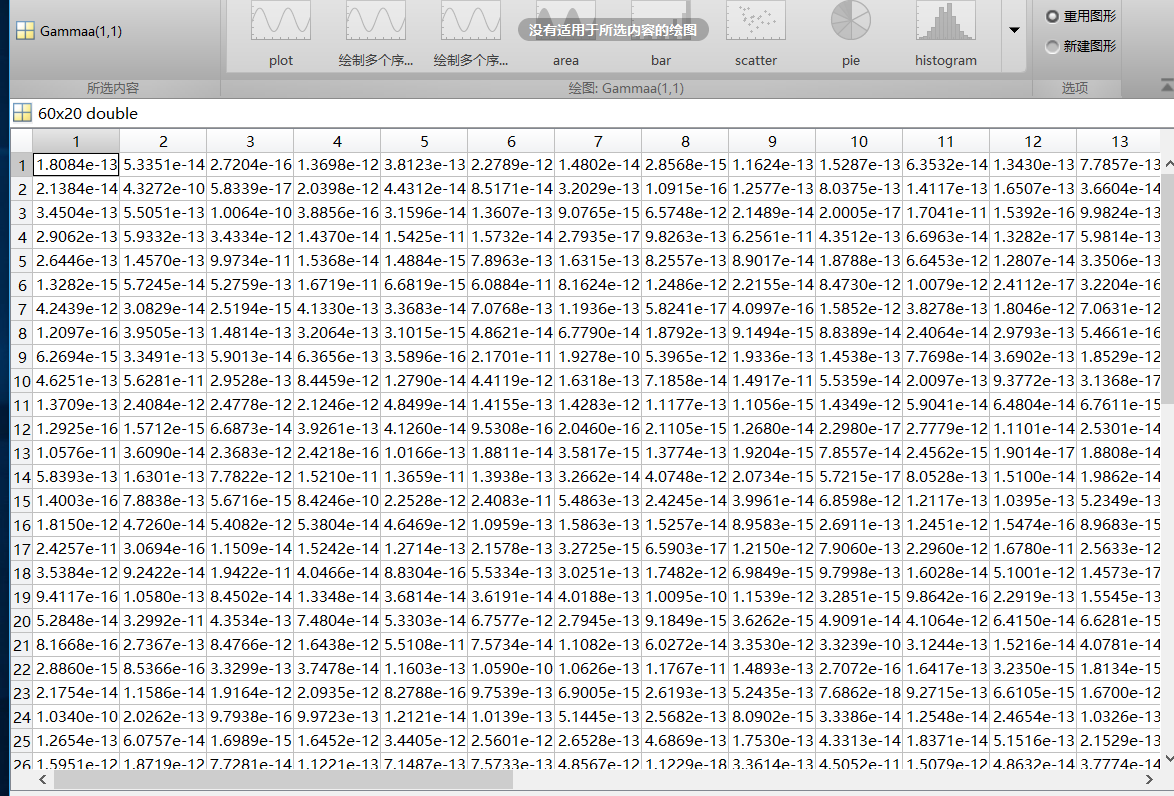
I put gamma data in the form of pictures,
just as you say, they have very extreme magnitudes (very close to 0),
The following is my result, under cvx2.1
————————————————————————————————————————————————
Calling SDPT3 4.0: 3621 variables, 1280 equality constraints
num. of constraints = 1280
dim. of sdp var = 2400, num. of sdp blk = 1200
dim. of linear var = 20
dim. of free var = 1 *** convert ublk to lblk
number of nearly dependent constraints = 60
To remove these constraints, re-run sqlp.m with OPTIONS.rmdepconstr = 1.
SDPT3: Infeasible path-following algorithms
version predcorr gam expon scale_data
HKM 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime
0|0.000|0.000|8.6e+00|2.0e+02|2.4e+05| 3.642686e-11 0.000000e+00| 0:0:01| spchol 1 1
1|0.000|0.000|8.6e+00|2.0e+02|3.7e+18| 3.642686e-11 -1.174478e+28| 0:0:01| spchol 1 2
2|0.000|0.000|8.6e+00|1.3e+04|8.3e+26| 4.035794e+00 -9.525936e+31| 0:0:01|
sqlp stop: primal or dual is diverging, 7.0e+17
number of iterations = 2
Total CPU time (secs) = 1.33
CPU time per iteration = 0.67
termination code = 3
DIMACS: 1.6e+02 0.0e+00 1.5e+04 0.0e+00 1.0e+00 8.7e-06
Status: Failed
Optimal value (cvx_optval): NaN
Calling Mosek 8.0.0.60: 3621 variables, 1280 equality constraints
MOSEK Version 8.0.0.60 (Build date: 2017-3-1 13:09:33)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (0) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (3) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (6) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (9) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (12) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (15) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (21) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (24) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (27) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (30) of matrix ‘A’.
Warning number 710 is disabled.
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 1280
Cones : 1200
Scalar variables : 3621
Matrix variables : 0
Integer variables : 0
Optimizer started.
Conic interior-point optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator - tries : 0 time : 0.00
Lin. dep. - tries : 1 time : 0.02
Lin. dep. - number : 0
Presolve terminated. Time: 0.03
Interior-point optimizer terminated. Time: 0.11.
MOSEK PRIMAL INFEASIBILITY REPORT.
Problem status: The problem is primal infeasible
Optimizer terminated. Time: 0.17
Interior-point solution summary
Problem status : PRIMAL_INFEASIBLE
Solution status : PRIMAL_INFEASIBLE_CER
Dual. obj: 1.0000000000e+000 nrm: 1e+000 Viol. con: 0e+000 var: 5e-011 cones: 0e+000
Optimizer summary
Optimizer - time: 0.17
Interior-point - iterations : 0 time: 0.11
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
Status: Infeasible
Optimal value (cvx_optval): -Inf
Calling SeDuMi 1.34: 3621 variables, 1280 equality constraints
SeDuMi 1.34 (beta) by AdvOL, 2005-2008 and Jos F. Sturm, 1998-2003.
Alg = 2: xz-corrector, Adaptive Step-Differentiation, theta = 0.250, beta = 0.500
Split 1 free variables
eqs m = 1280, order n = 2423, dim = 3623, blocks = 1201
nnz(A) = 6060 + 0, nnz(ADA) = 8860, nnz(L) = 5070
it : by gap delta rate t/tP t/tD* feas cg cg prec
0 : 8.36E-03 0.000
1 : -2.23E+05 2.79E-03 0.000 0.3340 0.9000 0.9000 -1.00 1 1 5.0E+00
2 : -3.36E+05 1.14E-03 0.000 0.4071 0.9000 0.9000 -1.00 19 19 5.0E+00
3 : -1.49E+05 2.23E-04 0.000 0.1958 0.0000 0.9000 -1.00 21 21 5.0E+00
4 : -1.72E+05 9.45E-05 0.000 0.4246 0.9121 0.9000 -1.00 20 20 5.0E+00
Run into numerical problems.
iter seconds digits cx by
4 1.9 -0.0 3.9627965484e+01 -1.7206323965e+05
|Ax-b| = 6.4e+01, [Ay-c]_+ = 1.8E+00, |x|= 1.5e+03, |y|= 1.5e+11
No sensible solution found.
Detailed timing (sec)
Pre IPM Post
5.540E-01 1.280E+00 7.900E-02
Max-norms: ||b||=1, ||c|| = 1,
Cholesky |add|=1, |skip| = 11, ||L.L|| = 1.
Status: Failed
Optimal value (cvx_optval): NaN
really really thank you