After the cvx finished the optimization, the expression values are not equal to the original constraint values

Amos · December 22, 2020, 12:45pm

I have a QCQP problem to be optimized.
After the cvx finished the optimization, the cvx_status is returned as “Solved”.
But I found that the optimized solution is a little strange.
So I tried to check the constraints.
My constraints are complicated, so I used the expression holder to contain my constraints.
I checked the optimized constraints, and they were all satisfied.
But when I checked the value of the original constraints, they were not satisfied the constraints.
Since my formulated problem is complicated, I show the simplified matlab code.

cvx_solver sedumi
cvx_precision best
cvx_begin quiet;
variable X(MB, K) complex;
expressions f6 f7(K) f8(L) f9;
… % The formulation of the expressions is omitted.
maximize(f6);
subject to
for k = 1 : K
f7(k) >= SINR_B;
end
for l = 1 : L
f8(l) >= SINR_S;
end
f9 <= P_B_max;
cvx_end;
cvx_status_W = cvx_status;

Specifically, the optimized f7 and f8 are all larger than the requied values.
But I recalculate the constraint values (not by the expression). I find that they are all less than the required values.
I am really confused.
I will really appreciate your response. Thanks a lot!

Mark_L_Stone · December 23, 2020, 2:43am

I found your post to be confusing.

After CVX completes, expressions and expression holders do not necessarily have their “optimal” (final) values. if you want to know the optimal (values) of expressions, you need to compute them starting from CVX variables, which will be at their optimal values.

Amos · December 23, 2020, 5:41am

Thanks for your response.
You said that the expressions and expression holders do not necessarily have their final values. But when I checked f7 and f8 after CVX completes, it returns with their values. I am confused whether they are the expression holders’ values.
And I computed the actual values of the inequalities’ left side with the CVX variable X(MB, K) in my code. They are not equal to the f7 and f8 values which returns to me before. Is it because that f7 and f8 values are not the expression holders’ final values?
Thanks for your response again.

Amos · December 23, 2020, 6:20am

Specifically, this is the f7 values.
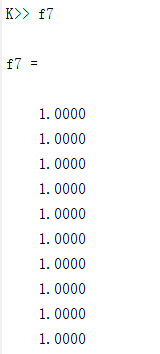
QQ截图20201223141305

Amos · December 23, 2020, 6:22am

This is the computed values with the CVX variables X(MB, K).
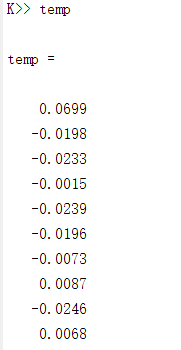
QQ截图20201223141336
The formulations are all the same. I had expected them to be equal. This is my confusion.
Thanks for your response again.

Mark_L_Stone · December 23, 2020, 1:51pm

In order to reliably have the optimal values of expressions after CVX completes, they must be reconstructed starting from CVX variable values. That is due to a design decision in CVX. CVX could have been designed to automatically do this, but it does not. However, the correct values of the expressions are used internally in performing the optimization.

Amos · December 23, 2020, 2:46pm

Thanks for your response.
I do not really understand what reconstructing the expressions starting from CVX variable values is. Could you explain it more specifically or give a simple framework of the optimization?
Really appreciating your response.

Mark_L_Stone · December 23, 2020, 2:52pm

In the code below, x is a variable, y is an expression, even though it is not declared an expression. Everything would be the same if expression y were inserted after variable x.

cvx_begin
variable x
y = x^2
minimize(x+y^2)
x >= 1
cvx_end
y % not guaranteed to have optimal value of y
y = x^2 % will have correct "optimal" value of y

Amos · December 24, 2020, 8:07am

Thanks for your detailed explaination.
Here is my code which is simplified from the original code.

cvx_begin
variable x
expressions y, z
y = f(x) % the expression y's construction
z = h(x) % the expression z's construction
maximize(y)
z >= 0
cvx_end
z % this value is larger than 0
z = h(x) % this value is not larger than 0

I reconstructed the expressions to check their values. But I found that the constraints were not satisfied with the reconstructed expressions’ values, while the cvx_status is Solved. I am confused about that.
Thanks for your response again.

Mark_L_Stone · December 24, 2020, 12:33pm

Please show the solver and CVX output, as well as your reconstruction calculations showing the constraints are not satisfied. Note that constraints are only guranateed to be satisfied to within a solver tolerance, such as 1e-8. Infeasibility by an amount less than that is still considered to be feasible.

Amos · December 25, 2020, 8:05am

Thanks for your response!
This is the cvx output.

Calling SeDuMi 1.3.4: 1516 variables, 620 equality constraints
   For improved efficiency, SeDuMi is solving the dual problem.
------------------------------------------------------------
SeDuMi 1.3.4 by AdvOL, 2005-2008 and Jos F. Sturm, 1998-2003.
Alg = 2: xz-corrector, Adaptive Step-Differentiation, theta = 0.250, beta = 0.500
eqs m = 620, order n = 617, dim = 1517, blocks = 301
nnz(A) = 20395 + 0, nnz(ADA) = 63192, nnz(L) = 40332
 it :     b*y       gap    delta  rate   t/tP*  t/tD*   feas cg cg  prec
  0 :            1.65E+11 0.000
  1 :   3.85E+11 9.84E+10 0.000 0.5947 0.9000 0.9000   6.59  1  1  4.6E+00
  2 :   3.35E+10 3.87E+10 0.000 0.3935 0.9000 0.9000   4.98  1  1  6.3E-01
  3 :  -9.18E+08 1.63E+09 0.000 0.0420 0.9900 0.9900   1.48  1  1  1.1E-01
  4 :  -4.30E+07 3.23E+07 0.000 0.0198 0.9900 0.9900   1.11  1  1  9.0E-02
  5 :  -6.59E+05 3.65E+05 0.350 0.0113 0.9945 0.9945   1.05  1  1  7.0E-02
  6 :  -1.36E+05 7.56E+04 0.000 0.2069 0.9000 0.9000   1.01  1  1  7.0E-02
  7 :  -8.78E+04 3.87E+04 0.000 0.5115 0.9592 0.9000   0.93  2  2  7.4E-02
  8 :  -1.04E+06 1.86E-19 0.000 0.0000 0.8950 0.9000   0.02  9  9  1.1E-06
  9 :  -1.35E+08 5.85E-22 0.000 0.0031 0.9990 0.9990  -0.85 13 13  7.7E-07
 10 :  -7.70E+09 1.86E-23 0.000 0.0318 0.9900 0.9900  -1.43 31 32  1.1E-06
 11 :  -1.44E+11 1.06E-24 0.000 0.0571 0.9900 0.9462  -1.02 29 31  1.1E-06
Run into numerical problems.

iter seconds digits       c*x               b*y
 11      0.4   Inf -1.5281375353e+11 -1.4420903211e+11
|Ax-b| =   3.7e+02, [Ay-c]_+ =   9.2E-07, |x|=  2.1e+17, |y|=  1.2e+05

Detailed timing (sec)
    Pre          IPM          Post
2.010E-01    6.300E-01    1.200E-02    
Max-norms: ||b||=1.425903e+10, ||c|| = 30,
Cholesky |add|=14, |skip| = 0, ||L.L|| = 500000.
------------------------------------------------------------
Status: Inaccurate/Solved
Optimal value (cvx_optval): -1.44209e+11

This is the original optimization code.

cvx_solver sedumi
cvx_begin
variable X(MB, K) complex;
expressions f6 f7(K) f8(L) f9;

%% The expressions' formulation
%% The variables such as a_, b_, and so on are pre-defined.
for k = 1 : K
    f6 = f6 + 2 * sqrt(1 + a_(k)) * real(alpha_(k)' * (f_d(:, k)' + phi' * F_r(:, :, k) * H_B) * X(:, k));
    for kk = 1 : K
        f6 = f6 - square_abs(alpha_(k)) * square_abs((f_d(:, k)' + phi' * F_r(:, :, k) * H_B) * X(:, kk));
    end
    for ll = 1 : L
        f6 = f6 - square_abs(alpha_(k)) * square_abs((g_i(:, k)' + phi' * F_r(:, :, k) * H_S) * W_S(:, ll));
    end
    f6 = f6 - square_abs(alpha_(k)) * Sigma2_B;
end
for l = 1 : L
    f6 = f6 + 2 * sqrt(1 + b_(l)) * real(beta_(l)' * (g_d(:, l)' + phi' * G_r(:, :, l) * H_S) * W_S(:, l));
    for ll = 1 : L
        f6 = f6 - square_abs(beta_(l)) * square_abs((g_d(:, l)' + phi' * G_r(:, :, l) * H_S) * W_S(:, ll));
    end
    for kk =1 : K
        f6 = f6 - square_abs(beta_(l)) * square_abs((f_i(:, l)' + phi' * G_r(:, :, l) * H_B) * X(:, kk));
    end
    f6 = f6 - square_abs(beta_(l)) * Sigma2_S;
end
for k = 1 : K
    f7(k) = f7(k) + 2 * real(p_(k)' * (f_d(:, k)' + phi' * F_r(:, :, k) * H_B) * X(:, k));
    for kk = 1 : K
        if kk ~= k
            f7(k) = f7(k) - square_abs(p_(k)) * square_abs((f_d(:, k)' + phi' * F_r(:, :, k) * H_B) * X(:, kk));
        end
    end
    for ll = 1 : L
        f7(k) = f7(k) - square_abs(p_(k)) * square_abs((g_i(:, k)' + phi' * F_r(:, :, k) * H_S) * W_S(:, ll));
    end
    f7(k) = f7(k) - square_abs(p_(k)) * Sigma2_B;
end
for l = 1 : L
    f8(l) = f8(l) + 2 * real(q_(l)' * (g_d(:, l)' + phi' * G_r(:, :, l) * H_S) * W_S(:, l));
    for ll = 1 : L
        if ll ~= l
            f8(l) = f8(l) - square_abs(q_(l)) * square_abs((g_d(:, l)' + phi' * G_r(:, :, l) * H_S) * W_S(:, ll));
        end
    end
    for kk = 1 : K
        f8(l) = f8(l) - square_abs(q_(l)) * square_abs((f_i(:, l )' + phi' * G_r(:, :, l) * H_B) * X(:, kk));
    end
    f8(l) = f8(l) - square_abs(q_(l)) * Sigma2_S;
end
for k = 1 : K
    f9 = f9 + X(:, k)' * X(:, k);
end

maximize(f6);
subject to
for k = 1 : K
    f7(k) >= SINR_B;
end
for l = 1 : L
    f8(l) >= SINR_S;
end
f9 <= P_B_max;
cvx_end;
cvx_status_W = cvx_status;

%% The reconstruction of the expressions.
%% The constraints with f7 and f8 are not satisfied.
f7 = zeros(K, 1);
f8 = zeros(L, 1);
f9 = 0;
for k = 1 : K
    f7(k) = f7(k) + 2 * real(p_(k)' * (f_d(:, k)' + phi' * F_r(:, :, k) * H_B) * X(:, k));
    for kk = 1 : K
        if kk ~= k
            f7(k) = f7(k) - square_abs(p_(k)) * square_abs((f_d(:, k)' + phi' * F_r(:, :, k) * H_B) * X(:, kk));
        end
    end
    for ll = 1 : L
        f7(k) = f7(k) - square_abs(p_(k)) * square_abs((g_i(:, k)' + phi' * F_r(:, :, k) * H_S) * W_S(:, ll));
    end
    f7(k) = f7(k) - square_abs(p_(k)) * Sigma2_B;
end
for l = 1 : L
    f8(l) = f8(l) + 2 * real(q_(l)' * (g_d(:, l)' + phi' * G_r(:, :, l) * H_S) * W_S(:, l));
    for ll = 1 : L
        if ll ~= l
            f8(l) = f8(l) - square_abs(q_(l)) * square_abs((g_d(:, l)' + phi' * G_r(:, :, l) * H_S) * W_S(:, ll));
        end
    end
    for kk = 1 : K
        f8(l) = f8(l) - square_abs(q_(l)) * square_abs((f_i(:, l )' + phi' * G_r(:, :, l) * H_B) * X(:, kk));
    end
    f8(l) = f8(l) - square_abs(q_(l)) * Sigma2_S;
end
for k = 1 : K
    f9 = f9 + X(:, k)' * X(:, k);
end

The problem is a little complicated. I think it may be the problem with the solver tolerance. Is there any solution to deal with the solver tolerance problem?
Thanks for your response again!

Mark_L_Stone · December 25, 2020, 1:17pm

You haven’;t shown your reconstruction calculations showing the constraints are not satisfied.

Nevertheless, the solver had numerical difficulty, and optimalobjective value of -1e11 indicates horrible scaling. you should change the units of input data to try to make non-zero input data within a few orders of magntiude of 1, and optimal objective value no greater in magnitude than perhaps 1e4 or 1e4. Certainly not 1e11. With horrible numbers such as these, and the solver having numerical difficulty and CVX reporting Inaccurate/solved, there could easily be large constraint violations.

I haven’t looked closely at your code, but when you have squares times other squares, there certainly is the potential for large magnitude numbers getting even larger; so care in model formulation is warranted.

Amos · December 26, 2020, 9:07am

Thanks for your response in this Christmas Day. And wish you a merry Christmas!
I think I need to scale the variables, objective and constraints properly then.
Thanks a lot!