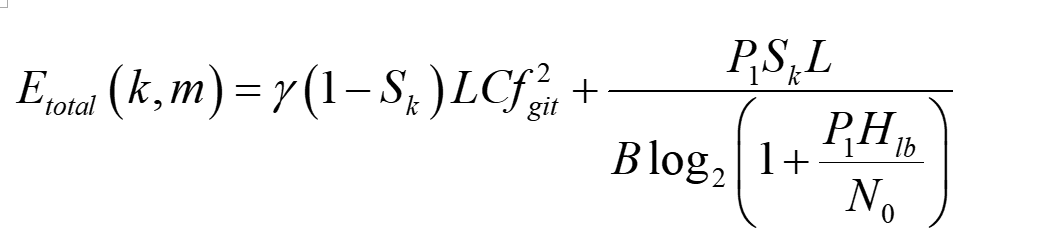That can happen due to transformations CVX uses, such as putting into epigraph form. In your case, some type of log or exp related function(s) were reformulated as exponential cone constraints…
I try to use CVXQUAD to solve this convex optimization problem,but it shows:
Using Pade approximation for exponential
cone with parameters m=3, k=3
Error using cvxprob/newcnstr (line 192)
Disciplined convex programming error:
Invalid constraint: {concave} == {real affine}
Error cvxprob/newcnstr (line 72)
newcnstr( prob, x{k}, y{k}, op );
Error == (line 3)
b = newcnstr( evalin( ‘caller’, ‘cvx_problem’, ‘[]’ ), x, y, ‘==’ );
Error cvx/rel_entr (line 80)
{ -q, xt, yt } == exponential( sz ); %#ok
Error testnewsolver (line 184)
Etotal(k,m)=gamac*(1-sk(k,m))LkCkf_gitf_git+P1sk(k,m)Lkinv_pos(B(-rel_entr(1,1+P1*Hlb(k,m)*inv_pos(N0)))*inv_pos(log(2)));
the expression of Etotal(k,m) shows below:
where Hlb(k,m) is a convex expression related to the optimization variable q(k,m),the others are constant.
In MATLAB,i wrote it this way
I don’t know why this error occurs?
Besides I don’t know why it shows" Using Pade approximation for exponential
cone with parameters m=3, k=3",is this related to the parameters m,k in Hlb(k,m)? But the parameter m in Hlb(k,m) increase from 0 to 50,and k increase from 0 to 6. So if it’s relevant, why m=3, k=3?
Using Pade approximation for exponential
cone with parameters m=3, k=3
is a message from CVXQUAD. m = 3, k = 3, are standard parameter values of its Pade approximation method.
As for the error message, in the future please show a complete reproducible problem, copy and pasted using Preformatted text icon, not posting an image of code.
You haven’t told us what the CVX variabes are, so I don’t even know if your expression is suitable for CVX. Are you able to enter your problem and have it accepted when CVXQUAD is not used? Are you only getting an error when reformulating log to rel_entr for CVXQUAD?
Your first step is to prove your optimization problem is convex.