Why are the constraints not satisfied over the optimized solution?

[11124 (yingyang)]

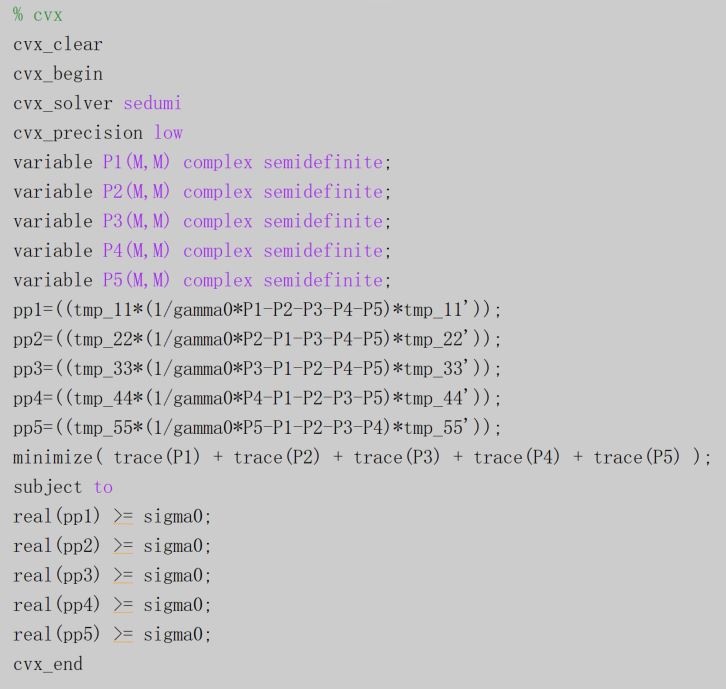
Why does the optimized solution fail to satisfy the original constraints? Could you give me any hint about this problem?

Calling SeDuMi 1.3.4: 25 variables, 5 equality constraints

SeDuMi 1.3.4 by AdvOL, 2005-2008 and Jos F. Sturm, 1998-2003.
Alg = 2: xz-corrector, Adaptive Step-Differentiation, theta = 0.250, beta = 0.500
eqs m = 5, order n = 16, dim = 26, blocks = 6
nnz(A) = 105 + 0, nnz(ADA) = 25, nnz(L) = 15
it : by gap delta rate t/tP t/tD* feas cg cg prec
0 : 9.31E+00 0.000
1 : 2.86E-13 7.55E-01 0.000 0.0811 0.9900 0.9900 2.55 1 1 6.9E-01
2 : 3.10E-13 2.03E-04 0.000 0.0003 0.9999 0.9999 1.01 1 1 6.7E-02
3 : 3.10E-13 2.10E-11 0.000 0.0000 1.0000 1.0000 1.00 1 1 6.9E-09

iter seconds digits cx by
3 0.2 6.2 1.3576927141e-11 3.1020033494e-13
|Ax-b| = 2.6e-12, [Ay-c]_+ = 0.0E+00, |x|= 4.0e-12, |y|= 3.5e+00

Detailed timing (sec)
Pre IPM Post
5.700E-02 8.999E-02 1.001E-02
Max-norms: ||b||=3.981072e-14, ||c|| = 2.000000e+00,
Cholesky |add|=0, |skip| = 0, ||L.L|| = 1.

Status: Solved
Optimal value (cvx_optval): +1.35769e-11

---

K>> pp1

pp1 =

-4.3325e-20 + 9.7837e-43i

K>> sigma0

sigma0 =

3.9811e-14

[Mark_L_Stone]

That is within solver feasibility tolerance, so is not considered to be a constraint violation. if you want to ensure pp1 is nonnegative, try using sigam0 = 1e-6 .

[11124 (yingyang)]

When setting sigma0=1e-6, the problem solving became infeasible, no matter what cvx_precision is set.

Calling SeDuMi 1.3.4: 25 variables, 5 equality constraints

SeDuMi 1.3.4 by AdvOL, 2005-2008 and Jos F. Sturm, 1998-2003.
Alg = 2: xz-corrector, Adaptive Step-Differentiation, theta = 0.250, beta = 0.500
eqs m = 5, order n = 16, dim = 26, blocks = 6
nnz(A) = 105 + 0, nnz(ADA) = 25, nnz(L) = 15
it : by gap delta rate t/tP t/tD* feas cg cg prec
0 : 9.31E+00 0.000
1 : 7.19E-06 7.55E-01 0.000 0.0811 0.9900 0.9900 2.55 1 1 6.9E-01
2 : 7.79E-06 1.95E-04 0.000 0.0003 0.9999 0.9999 1.01 1 1 6.3E-02
3 : 1.00E-05 1.82E-05 0.000 0.0936 0.9900 0.9900 0.91 1 1 5.3E-03
4 : 2.54E-04 5.48E-06 0.000 0.3006 0.9000 0.9000 -0.69 1 1 1.3E-05
5 : 1.53E-02 3.29E-08 0.000 0.0060 0.9990 0.9990 -0.73 1 1 4.5E-06
6 : 5.10E+01 1.13E-11 0.000 0.0003 0.9999 0.9999 -1.00 1 1 5.2E-06
7 : 2.14E+02 3.46E-12 0.000 0.3052 0.9000 0.9000 -1.26 1 1 6.6E-06
8 : 6.32E+02 1.35E-12 0.000 0.3905 0.9000 0.9000 -1.32 1 1 7.6E-06
9 : 2.54E+03 4.68E-13 0.000 0.3460 0.9000 0.9000 -1.56 1 1 1.1E-05
10 : 2.54E+04 9.97E-14 0.000 0.2132 0.9000 0.9000 -1.88 1 1 2.3E-05
11 : 1.55E+06 6.67E-16 0.000 0.0067 0.9990 0.9990 -1.29 1 1 9.2E-06
12 : 1.55E+13 1.70E-22 0.000 0.0000 1.0000 1.0000 -1.00 1 1
Primal infeasible, dual improving direction found.
iter seconds |Ax| [Ay]_+ |x| |y|
12 0.1 0.0e+00 0.0e+00 0.0e+00 4.9e+05

Detailed timing (sec)
Pre IPM Post
1.600E-02 4.800E-02 2.002E-03
Max-norms: ||b||=1.000000e-06, ||c|| = 2.000000e+00,
Cholesky |add|=0, |skip| = 0, ||L.L|| = 2.52691.

Status: Infeasible
Optimal value (cvx_optval): +Inf

[Mark_L_Stone]

Please show a reproducilble problem, complete with all input data.

It may be that the only feasible solution is P1 = P2 = P2 = P3 = P5 = P5 = matrix of all zeros.

You could try sigma0 = 1e-8 and you can also try another solver, such as SeDuMi, or Mosek if you have it,