Using different solvers to solve a problem and get multiple answers

1

this is my code：
function [Pr,R] = SolvePower(Qr)
L=2000;
gama=10^8;
H=100;
d=10*ones(1,20);
T=100;
tol=0.001;
ws=zeros(2,20);
for m = 1:1:20
wd(1,m)=2000;
wd(2,m)=0;
end
M=20;
N=20;
load Q12
save Q12
Ql=Q12;
% Q12(:,1:10,1)=[960,920,880,840,800,760,720,680,640,600;360,320,280,240,200,160,120,80,40,0];
% Q12(:,11:20,1)=[640,680,720,760,800,840,880,920,960,1000;-40,-80,-120,-160,-200,-240,-280,-320,-360,-380];
% Q12(:,1:10,2)= [1040,1080,1120,1160,1200,1240,1280,1320,1360,1400;360,320,280,240,200,160,120,80,40,0];
% Q12(:,11:20,2)=[1360,1320,1280,1240,1200,1160,1120,1080,1040,1020;-40,-80,-120,-160,-200,-240,-280,-320,-360,-390];

R=[];
P=10*ones(3,M);
P(1,19)=0;%P1 source
P(1,20)=0;
P(2,1)=0;%UAV1
P(2,20)=0;
P(3,1)=0;%UAV2
P(3,2)=0;
gama_s=P(1,:)*gama;
gama_1=P(2,:)*gama;
gama_2=P(3,:)*gama;

for l=1:1:100

iteration=l

cvx_begin
% cvx_solver mosek
variable Q(2,M,2)
variable u(2,M)
expression alpha_s(1,M)
expression R_q1_lb(1,M)
expression alpha_12(1,M)
expression beta_12(1,M)
expression R_qlq2_lb(1,M)
expression alpha_2(1,M)
expression beta_2(1,M)
expression R_d_lb(1,M)

for m=1:1:20

alpha_s(m)=log2 ( 1+ (gama_s(m)./( (H)^2 +(sum_square(Ql(:,m,1)-ws(:,m))))) );
beta_1(m)=log2(exp(1))gama_s(m) ./ ( ((H^2 +gama_s(m)+sum_square(Ql(:,m,1)-ws(:,m))) (H^2+sum_square(Ql(:,m,1)-ws(:,m)))));
R_q1_lb(m)=alpha_s(m)-beta_1(m)*( sum_square(Q(:,m,1)-ws(:,m))-sum_square(Ql(:,m,1)-ws(:,m)));

alpha_12(m)=log2( 1+ (gama_1(m)./( sum_square(Ql(:,m,2)-Ql(:,m,1)))) );
beta_12(m)=log2(exp(1))gama_1(m) ./ ( (gama_1(m) +sum_square(Ql(:,m,2)-Ql(:,m,1)))(sum_square(Ql(:,m,2)-Ql(:,m,1))));
R_qlq2_lb(m)=alpha_12(m)-beta_12(m)*(sum_square(Q(:,m,2)-Q(:,m,1))-sum_square(Ql(:,m,2)-Ql(:,m,1)));

alpha_2(m)=log2(1+ (gama_2(m)./ (H^2 +(sum_square(wd(:,m)-Ql(:,m,2))))));
beta_2(m)=log2(exp(1))gama_2(m) ./ ((H^2 +gama_2(m) + sum_square(wd(:,m)-Ql(:,m,2)))(H^2+sum_square(wd(:,m)-Ql(:,m,2))));
R_d_lb(m)=alpha_2(m)-beta_2(m)*(sum_square(wd(:,m)-Q(:,m,2)) -sum_square(wd(:,m)-Ql(:,m,2)));

end

maximize sum(u(2,:))
subject to
sum(u(1,:))<=sum(R_q1_lb(1:19));
sum(u(2,:))<=sum(u(1,1:19));
u(1,:)<=R_qlq2_lb(1,:);
u(2,:)<=R_d_lb(1,:);

for m=1:1:20
% u(1,m)<=R_qlq2_lb(m);
% u(2,m)<=R_d_lb(m);
d(m).^2 <= -sum_square(Ql(:,m,2)-Ql(:,m,1)) +2*(Ql(:,m,2)-Ql(:,m,1))’ *(Q(:,m,2)-Q(:,m,1))
end

norm(Q(:,1,1)-[1000;400]) <=50;
norm(Q(:,1,2)-[1000;400]) <=50;

norm([1000;-400]-Q(:,20,1))<=50;
norm([1000;-400]-Q(:,20,2))<=50;

for m=1:1:19
norm(Q(:,m+1,2)-Q(:,m,2))<=50
norm(Q(:,m+1,1)-Q(:,m,1))<=50
end
cvx_end
Ql=Q;

R_ite=sum(u(2,:));

save Ql
R=[R;R_ite];
if (l >= 2) &&(R(l) - R(l-1) < tol)
break
end

end
load Ql
size(Ql)
m=1:1:20;
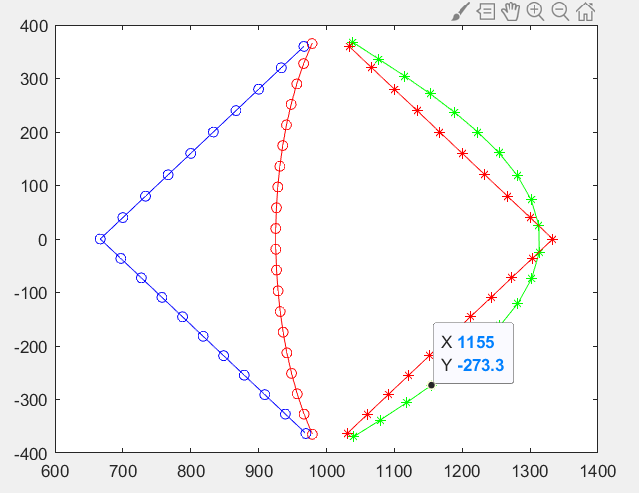
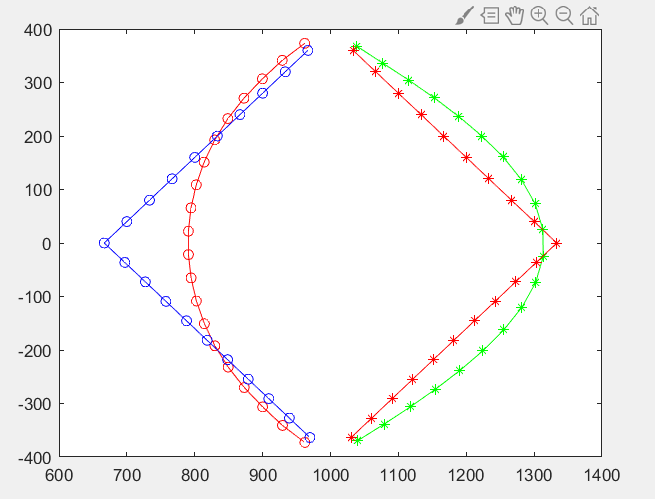
plot(Ql(1,m,1),Ql(2,m,1),‘r-o’,Ql(1,m,2),Ql(2,m,2),‘g-’);
hold on
plot(Q12(1,m,1),Q12(2,m,1),‘b-o’,Q12(1,m,2),Q12(2,m,2),'r-’)
end

the objecttive and constraints Has been processed with SCA algorithm，so，this is a convex optimization，which including norm constrains，it is a SOCP ，I found mosek ，sedumi and sdpt3 can solve it，when I changed the solver（because I am not satisfied with the result），I found with different solver，there may have the same Optimal value (cvx_optval)，but the optimized variables are different，this is the details：
sdpt3:
Calling SDPT3 4.0: 470 variables, 248 equality constraints

num. of constraints = 248
dim. of socp var = 366, num. of socp blk = 102
dim. of linear var = 104
2 linear variables from unrestricted variable.
*** convert ublk to lblk

SDPT3: Infeasible path-following algorithms

version predcorr gam expon scale_data
NT 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime

0|0.000|0.000|3.7e+01|3.5e+03|1.2e+10| 2.266130e+08 0.000000e+00| 0:0:00| chol 1 1
1|0.661|0.207|1.3e+01|2.8e+03|6.7e+09| 1.392855e+08 -3.994785e+06| 0:0:00| chol 1 1
2|0.787|0.532|2.7e+00|1.3e+03|2.9e+09| 1.415497e+08 2.079809e+07| 0:0:00| chol 1 1
3|0.656|0.798|9.3e-01|2.6e+02|8.3e+08| 1.276343e+08 1.894135e+07| 0:0:00| chol 1 1
4|0.655|0.583|3.2e-01|1.1e+02|3.6e+08| 8.594728e+07 2.746142e+07| 0:0:00| chol 1 1
5|0.508|0.516|1.6e-01|5.3e+01|2.0e+08| 5.579132e+07 3.993011e+07| 0:0:00| chol 1 1
6|0.438|0.437|8.9e-02|3.0e+01|1.3e+08| 3.698776e+07 4.368700e+07| 0:0:00| chol 1 1
7|0.512|0.481|4.3e-02|1.5e+01|7.5e+07| 2.189730e+07 3.850608e+07| 0:0:00| chol 1 1
8|0.567|0.551|1.9e-02|6.9e+00|4.0e+07| 1.164572e+07 2.767425e+07| 0:0:00| chol 1 1
9|0.684|0.303|5.9e-03|4.8e+00|2.3e+07| 4.745656e+06 2.045168e+07| 0:0:00| chol 1 1
10|0.695|0.760|1.8e-03|1.2e+00|7.4e+06| 1.928667e+06 5.673370e+06| 0:0:00| chol 1 1
11|0.342|0.294|1.2e-03|8.2e-01|5.6e+06| 1.414620e+06 4.226789e+06| 0:0:00| chol 1 1
12|0.485|0.492|6.1e-04|4.1e-01|3.5e+06| 8.877965e+05 2.095398e+06| 0:0:00| chol 1 1
13|0.552|0.525|2.8e-04|2.0e-01|2.0e+06| 5.030268e+05 9.652673e+05| 0:0:00| chol 1 1
14|0.676|0.459|8.9e-05|1.1e-01|1.0e+06| 2.229816e+05 4.800018e+05| 0:0:00| chol 1 1
15|0.754|0.369|2.2e-05|6.7e-02|5.4e+05| 7.615889e+04 2.785683e+05| 0:0:00| chol 1 1
16|1.000|0.752|1.1e-10|1.7e-02|1.2e+05| 3.302983e+03 5.504937e+04| 0:0:00| chol 1 1
17|0.984|0.986|1.2e-10|2.4e-04|1.7e+03| 1.204111e+02 8.643610e+02| 0:0:00| chol 1 1
18|0.818|0.948|1.4e-10|1.5e-05|1.1e+02| 7.908718e+01 1.277494e+02| 0:0:00| chol 1 1
19|1.000|0.752|1.4e-10|5.0e-06|2.9e+01| 7.468594e+01 9.491371e+01| 0:0:00| chol 1 1
20|1.000|0.587|1.9e-10|2.2e-06|1.1e+01| 7.182325e+01 8.172272e+01| 0:0:00| chol 1 1
21|0.972|0.943|2.4e-10|1.4e-07|6.4e-01| 7.148115e+01 7.217183e+01| 0:0:00| chol 1 1
22|0.976|0.837|1.7e-10|2.5e-08|1.0e-01| 7.146102e+01 7.158743e+01| 0:0:00| chol 1 1
23|1.000|0.050|2.4e-10|2.3e-08|9.8e-02| 7.146097e+01 7.158102e+01| 0:0:00| chol 1 1
24|1.000|0.745|1.7e-10|6.0e-09|2.5e-02| 7.145974e+01 7.149049e+01| 0:0:00| chol 1 1
25|1.000|0.736|1.7e-10|8.5e-08|7.0e-03| 7.145956e+01 7.146771e+01| 0:0:00| chol 1 1
26|1.000|0.896|1.4e-10|1.0e-07|8.5e-04| 7.145954e+01 7.146035e+01| 0:0:00| chol 1 1
27|0.906|0.915|2.4e-10|5.0e-08|2.3e-04| 7.145955e+01 7.145949e+01| 0:0:00| chol 2 2
28|1.000|0.493|1.3e-08|4.5e-08|1.4e-04| 7.145952e+01 7.145948e+01| 0:0:00| chol 1 2
29|1.000|0.490|9.4e-09|2.7e-08|8.9e-05| 7.145952e+01 7.145949e+01| 0:0:00| chol 1 1
30|1.000|0.491|9.4e-09|1.8e-08|5.8e-05| 7.145951e+01 7.145949e+01| 0:0:01| chol 1 1
31|1.000|0.494|3.7e-09|1.2e-08|3.8e-05| 7.145951e+01 7.145950e+01| 0:0:01| chol 1 1
32|1.000|0.497|2.5e-09|7.9e-09|2.5e-05| 7.145951e+01 7.145950e+01| 0:0:01| chol 1 1
33|1.000|0.500|1.7e-09|5.1e-09|1.6e-05| 7.145951e+01 7.145950e+01| 0:0:01| chol 1 1
34|1.000|0.503|2.4e-09|3.3e-09|1.0e-05| 7.145951e+01 7.145950e+01| 0:0:01| chol 1 1
35|1.000|0.507|6.1e-10|2.1e-09|6.6e-06| 7.145951e+01 7.145951e+01| 0:0:01| chol 1 1
36|1.000|0.510|8.9e-10|1.4e-09|4.2e-06| 7.145951e+01 7.145951e+01| 0:0:01| chol 1 1
37|1.000|0.514|4.9e-10|8.7e-10|2.7e-06| 7.145951e+01 7.145951e+01| 0:0:01| chol 1 1
38|1.000|0.517|3.3e-10|5.5e-10|1.7e-06| 7.145951e+01 7.145951e+01| 0:0:01|
stop: max(relative gap, infeasibilities) < 1.49e-08

number of iterations = 38
primal objective value = 7.14595079e+01
dual objective value = 7.14595070e+01
gap := trace(XZ) = 1.68e-06
relative gap = 1.17e-08
actual relative gap = 6.28e-09
rel. primal infeas (scaled problem) = 3.28e-10
rel. dual " " " = 5.52e-10
rel. primal infeas (unscaled problem) = 0.00e+00
rel. dual " " " = 0.00e+00
norm(X), norm(y), norm(Z) = 5.6e+06, 5.9e+00, 9.3e+00
norm(A), norm(b), norm© = 5.0e+03, 6.2e+06, 5.5e+00
Total CPU time (secs) = 0.64
CPU time per iteration = 0.02
termination code = 0
DIMACS: 9.1e-10 0.0e+00 1.5e-09 0.0e+00 6.3e-09 1.2e-08

Status: Solved
Optimal value (cvx_optval): +189.852

iteration =
2

Calling SDPT3 4.0: 470 variables, 248 equality constraints

num. of constraints = 248
dim. of socp var = 366, num. of socp blk = 102
dim. of linear var = 104
2 linear variables from unrestricted variable.
*** convert ublk to lblk

SDPT3: Infeasible path-following algorithms

version predcorr gam expon scale_data
NT 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime

0|0.000|0.000|3.3e+01|2.2e+03|8.4e+09| 1.558393e+08 0.000000e+00| 0:0:00| chol 1 1
1|0.660|0.207|1.1e+01|1.8e+03|4.6e+09| 9.583035e+07 -3.608047e+06| 0:0:00| chol 1 1
2|0.785|0.539|2.4e+00|8.2e+02|2.0e+09| 9.744673e+07 1.125972e+07| 0:0:00| chol 1 1
3|0.669|0.790|7.9e-01|1.7e+02|5.8e+08| 8.758777e+07 9.628872e+06| 0:0:00| chol 1 1
4|0.657|0.591|2.7e-01|7.0e+01|2.5e+08| 5.926966e+07 1.727079e+07| 0:0:00| chol 1 1
5|0.505|0.576|1.3e-01|3.0e+01|1.3e+08| 3.858818e+07 2.613284e+07| 0:0:00| chol 1 1
6|0.504|0.478|6.7e-02|1.6e+01|7.6e+07| 2.329016e+07 2.512541e+07| 0:0:00| chol 1 1
7|0.539|0.525|3.1e-02|7.4e+00|4.2e+07| 1.300610e+07 2.128926e+07| 0:0:00| chol 1 1
8|0.612|0.568|1.2e-02|3.2e+00|2.1e+07| 6.276221e+06 1.371173e+07| 0:0:00| chol 1 1
9|0.740|0.589|3.1e-03|1.3e+00|8.6e+06| 2.263387e+06 6.297315e+06| 0:0:00| chol 1 1
10|0.480|0.517|1.6e-03|6.4e-01|5.1e+06| 1.366910e+06 3.044395e+06| 0:0:00| chol 1 1
11|0.477|0.565|8.4e-04|2.8e-01|3.1e+06| 8.502038e+05 1.192538e+06| 0:0:00| chol 1 1
12|0.638|0.288|3.1e-04|2.0e-01|1.9e+06| 4.014555e+05 8.237916e+05| 0:0:00| chol 1 1
13|0.647|0.488|1.1e-04|1.0e-01|9.6e+05| 1.895871e+05 4.155112e+05| 0:0:00| chol 1 1
14|0.781|0.402|2.4e-05|6.0e-02|5.0e+05| 5.941252e+04 2.264221e+05| 0:0:00| chol 1 1
15|1.000|0.776|1.1e-10|1.4e-02|1.1e+05| 2.694184e+03 4.037199e+04| 0:0:00| chol 1 1
16|0.987|0.986|1.0e-10|2.0e-04|1.5e+03| 1.222631e+02 7.417497e+02| 0:0:00| chol 1 1
17|0.810|0.933|1.1e-10|2.0e-05|1.3e+02| 8.952063e+01 1.646822e+02| 0:0:00| chol 1 1
18|1.000|0.870|8.3e-11|5.7e-06|2.1e+01| 8.559144e+01 1.149131e+02| 0:0:00| chol 1 1
19|1.000|0.315|2.0e-10|4.5e-06|1.3e+01| 8.302983e+01 1.083068e+02| 0:0:00| chol 1 1
20|0.971|0.962|2.8e-10|3.5e-07|5.8e-01| 8.227594e+01 8.451644e+01| 0:0:00| chol 1 1
21|0.966|0.926|3.9e-10|4.4e-08|4.6e-02| 8.223064e+01 8.252467e+01| 0:0:00| chol 1 1
22|1.000|0.880|8.4e-10|2.1e-07|6.8e-03| 8.222911e+01 8.227600e+01| 0:0:00| chol 1 1
23|1.000|0.962|9.2e-10|1.3e-07|5.6e-04| 8.222894e+01 8.223050e+01| 0:0:00| chol 1 1
24|0.938|0.884|2.7e-09|4.8e-08|6.9e-05| 8.222886e+01 8.222904e+01| 0:0:00| chol 1 1
25|1.000|0.489|3.4e-09|1.4e-08|4.5e-05| 8.222886e+01 8.222895e+01| 0:0:00| chol 1 1
26|1.000|0.487|5.7e-09|9.1e-09|2.9e-05| 8.222886e+01 8.222890e+01| 0:0:00| chol 1 1
27|1.000|0.487|2.8e-09|6.1e-09|1.9e-05| 8.222886e+01 8.222887e+01| 0:0:00| chol 1 1
28|1.000|0.488|2.0e-09|4.1e-09|1.3e-05| 8.222886e+01 8.222886e+01| 0:0:00| chol 1 1
29|1.000|0.488|1.2e-09|2.7e-09|8.4e-06| 8.222885e+01 8.222886e+01| 0:0:00| chol 1 1
30|1.000|0.489|5.4e-10|1.8e-09|5.5e-06| 8.222885e+01 8.222886e+01| 0:0:00| chol 1 1
31|1.000|0.491|5.5e-10|1.2e-09|3.6e-06| 8.222885e+01 8.222885e+01| 0:0:01| chol 1 1
32|1.000|0.492|4.8e-10|7.9e-10|2.4e-06| 8.222885e+01 8.222885e+01| 0:0:01|
stop: max(relative gap, infeasibilities) < 1.49e-08

number of iterations = 32
primal objective value = 8.22288541e+01
dual objective value = 8.22288538e+01
gap := trace(XZ) = 2.38e-06
relative gap = 1.44e-08
actual relative gap = 1.63e-09
rel. primal infeas (scaled problem) = 4.79e-10
rel. dual " " " = 7.91e-10
rel. primal infeas (unscaled problem) = 0.00e+00
rel. dual " " " = 0.00e+00
norm(X), norm(y), norm(Z) = 4.2e+06, 6.1e+00, 9.6e+00
norm(A), norm(b), norm© = 3.8e+03, 4.9e+06, 5.5e+00
Total CPU time (secs) = 0.53
CPU time per iteration = 0.02
termination code = 0
DIMACS: 1.5e-09 0.0e+00 2.2e-09 0.0e+00 1.6e-09 1.4e-08

Status: Solved
Optimal value (cvx_optval): +189.889

iteration =
3

Calling SDPT3 4.0: 470 variables, 248 equality constraints

num. of constraints = 248
dim. of socp var = 366, num. of socp blk = 102
dim. of linear var = 104
2 linear variables from unrestricted variable.
*** convert ublk to lblk

SDPT3: Infeasible path-following algorithms

version predcorr gam expon scale_data
NT 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime

0|0.000|0.000|3.2e+01|2.1e+03|7.9e+09| 1.462710e+08 0.000000e+00| 0:0:00| chol 1 1
1|0.660|0.207|1.1e+01|1.7e+03|4.4e+09| 8.993829e+07 -3.499728e+06| 0:0:00| chol 1 1
2|0.788|0.540|2.3e+00|7.6e+02|1.8e+09| 9.146250e+07 1.009631e+07| 0:0:00| chol 1 1
3|0.671|0.788|7.7e-01|1.6e+02|5.4e+08| 8.213190e+07 8.917568e+06| 0:0:00| chol 1 1
4|0.656|0.606|2.6e-01|6.4e+01|2.3e+08| 5.573292e+07 1.645272e+07| 0:0:00| chol 1 1
5|0.511|0.568|1.3e-01|2.7e+01|1.2e+08| 3.581814e+07 2.414773e+07| 0:0:00| chol 1 1
6|0.494|0.474|6.6e-02|1.4e+01|7.1e+07| 2.185661e+07 2.359768e+07| 0:0:00| chol 1 1
7|0.538|0.521|3.0e-02|6.9e+00|4.0e+07| 1.224035e+07 1.979888e+07| 0:0:00| chol 1 1
8|0.616|0.573|1.2e-02|3.0e+00|1.9e+07| 5.864515e+06 1.279922e+07| 0:0:00| chol 1 1
9|0.732|0.573|3.1e-03|1.3e+00|8.2e+06| 2.146324e+06 6.001597e+06| 0:0:00| chol 1 1
10|0.495|0.490|1.6e-03|6.4e-01|4.9e+06| 1.276047e+06 3.102329e+06| 0:0:00| chol 1 1
11|0.482|0.544|8.1e-04|2.9e-01|3.0e+06| 7.957656e+05 1.323794e+06| 0:0:00| chol 1 1
12|0.622|0.290|3.1e-04|2.1e-01|1.9e+06| 3.913500e+05 9.198335e+05| 0:0:00| chol 1 1
13|0.641|0.495|1.1e-04|1.1e-01|9.6e+05| 1.869496e+05 4.565074e+05| 0:0:00| chol 1 1
14|0.783|0.387|2.4e-05|6.5e-02|5.1e+05| 5.880196e+04 2.582131e+05| 0:0:00| chol 1 1
15|1.000|0.783|1.0e-10|1.4e-02|1.0e+05| 2.689995e+03 4.584608e+04| 0:0:00| chol 1 1
16|0.987|0.986|1.2e-10|2.1e-04|1.5e+03| 1.291976e+02 8.229182e+02| 0:0:00| chol 1 1
17|0.805|0.928|1.2e-10|2.1e-05|1.3e+02| 9.214076e+01 1.761121e+02| 0:0:00| chol 1 1
18|1.000|0.528|1.2e-10|1.2e-05|6.2e+01| 8.889467e+01 1.403238e+02| 0:0:00| chol 1 1
19|1.000|0.789|1.4e-10|3.9e-06|1.4e+01| 8.581932e+01 1.071055e+02| 0:0:00| chol 1 1
20|0.937|0.821|2.3e-10|8.5e-07|2.5e+00| 8.504127e+01 8.999084e+01| 0:0:00| chol 1 1
21|0.976|0.859|2.4e-10|1.4e-07|3.4e-01| 8.494854e+01 8.577426e+01| 0:0:01| chol 1 1
22|1.000|0.085|2.5e-10|1.3e-07|3.1e-01| 8.494764e+01 8.570406e+01| 0:0:01| chol 1 1
23|1.000|0.769|2.5e-10|2.9e-08|7.3e-02| 8.494366e+01 8.511913e+01| 0:0:01| chol 1 1
24|1.000|0.724|2.4e-10|8.1e-09|2.0e-02| 8.494320e+01 8.499167e+01| 0:0:01| chol 1 1
25|1.000|0.213|2.6e-10|7.8e-08|1.7e-02| 8.494315e+01 8.498130e+01| 0:0:01| chol 1 1
26|1.000|0.919|2.7e-10|2.7e-07|1.6e-03| 8.494313e+01 8.494610e+01| 0:0:01| chol 1 1
27|1.000|0.928|2.0e-10|1.1e-07|3.2e-04| 8.494313e+01 8.494317e+01| 0:0:01| chol 1 1
28|1.000|0.490|4.3e-09|6.3e-08|1.9e-04| 8.494309e+01 8.494310e+01| 0:0:01| chol 1 1
29|1.000|0.488|3.9e-09|3.8e-08|1.2e-04| 8.494308e+01 8.494307e+01| 0:0:01| chol 1 1
30|1.000|0.489|2.5e-09|2.5e-08|8.1e-05| 8.494308e+01 8.494306e+01| 0:0:01| chol 1 1
31|1.000|0.491|1.1e-09|1.7e-08|5.3e-05| 8.494308e+01 8.494306e+01| 0:0:01| chol 1 1
32|1.000|0.493|1.2e-09|1.1e-08|3.5e-05| 8.494307e+01 8.494306e+01| 0:0:01| chol 1 1
33|1.000|0.495|5.0e-10|7.4e-09|2.3e-05| 8.494307e+01 8.494306e+01| 0:0:01| chol 1 1
34|1.000|0.498|4.6e-10|4.8e-09|1.5e-05| 8.494307e+01 8.494307e+01| 0:0:01| chol 1 1
35|1.000|0.501|4.5e-10|3.1e-09|9.5e-06| 8.494307e+01 8.494307e+01| 0:0:01| chol 1 1
36|1.000|0.504|2.8e-10|2.0e-09|6.1e-06| 8.494307e+01 8.494307e+01| 0:0:01| chol 1 1
37|1.000|0.507|1.1e-10|1.3e-09|3.9e-06| 8.494307e+01 8.494307e+01| 0:0:01| chol 1 1
38|1.000|0.510|8.5e-11|8.3e-10|2.5e-06| 8.494307e+01 8.494307e+01| 0:0:01|
stop: max(relative gap, infeasibilities) < 1.49e-08

number of iterations = 38
primal objective value = 8.49430708e+01
dual objective value = 8.49430695e+01
gap := trace(XZ) = 2.51e-06
relative gap = 1.47e-08
actual relative gap = 7.42e-09
rel. primal infeas (scaled problem) = 8.48e-11
rel. dual " " " = 8.33e-10
rel. primal infeas (unscaled problem) = 0.00e+00
rel. dual " " " = 0.00e+00
norm(X), norm(y), norm(Z) = 5.2e+06, 6.1e+00, 9.6e+00
norm(A), norm(b), norm© = 3.6e+03, 4.6e+06, 5.5e+00
Total CPU time (secs) = 0.77
CPU time per iteration = 0.02
termination code = 0
DIMACS: 2.7e-10 0.0e+00 2.3e-09 0.0e+00 7.4e-09 1.5e-08

Status: Solved
Optimal value (cvx_optval): +189.889
This is the optimized variables：image

2

MOSEK：
Calling Mosek 9.1.9: 470 variables, 248 equality constraints

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:34:40)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86

MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (13) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (21) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (25) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (33) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (49) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (57) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (61) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (69) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (85) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (93) of matrix ‘A’.
Warning number 710 is disabled.
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 248
Cones : 102
Scalar variables : 470
Matrix variables : 0
Integer variables : 0

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 42
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 2 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.00
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 248
Cones : 102
Scalar variables : 470
Matrix variables : 0
Integer variables : 0

Optimizer - threads : 2
Optimizer - solved problem : the primal
Optimizer - Constraints : 205
Optimizer - Cones : 102
Optimizer - Scalar variables : 388 conic : 366
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 1397 after factor : 1748
Factor - dense dim. : 0 flops : 2.24e+04
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 2.0e+03 1.0e+00 2.1e+03 0.00e+00 7.501932094e-04 -2.099999644e+03 1.0e+00 0.00
1 3.2e+02 1.6e-01 8.4e+02 -1.00e+00 5.290697134e+00 -2.087251414e+03 1.6e-01 0.03
2 7.2e+01 3.6e-02 4.0e+02 -9.98e-01 2.690364452e+01 -2.039587426e+03 3.6e-02 0.03
3 1.5e+01 7.3e-03 1.8e+02 -9.96e-01 1.346676778e+02 -1.811140629e+03 7.3e-03 0.03
4 2.7e+00 1.4e-03 7.5e+01 -9.87e-01 7.122879750e+02 -6.166920345e+02 1.4e-03 0.03
5 6.5e-01 3.3e-04 3.6e+01 -9.61e-01 2.772471331e+03 3.534687566e+03 3.3e-04 0.05
6 2.1e-01 1.0e-04 1.9e+01 -9.12e-01 7.978450891e+03 1.373083116e+04 1.0e-04 0.05
7 5.0e-02 2.5e-05 7.9e+00 -8.29e-01 2.529223657e+04 4.633796402e+04 2.5e-05 0.05
8 3.0e-02 1.5e-05 5.5e+00 -6.29e-01 3.540251623e+04 6.389768618e+04 1.5e-05 0.05
9 6.5e-03 3.3e-06 1.5e+00 -4.95e-01 6.793880370e+04 1.147255034e+05 3.3e-06 0.05
10 1.4e-03 7.2e-07 2.0e-01 1.98e-01 3.817505468e+04 5.620755345e+04 7.2e-07 0.05
11 7.2e-05 3.6e-08 2.2e-03 8.20e-01 2.799916340e+03 3.649009811e+03 3.6e-08 0.05
12 1.3e-07 6.5e-11 1.5e-07 9.99e-01 8.256561222e+01 8.377748686e+01 6.5e-11 0.05
13 2.0e-08 9.9e-12 9.7e-09 1.06e+00 7.751933643e+01 7.773323597e+01 9.9e-12 0.05
14 1.6e-09 7.8e-13 2.0e-10 1.06e+00 7.214283252e+01 7.215783185e+01 7.8e-13 0.05
15 5.3e-11 2.5e-14 1.2e-12 1.01e+00 7.148107986e+01 7.148156339e+01 2.5e-14 0.06
16 1.1e-11 1.3e-15 8.5e-15 1.00e+00 7.146059320e+01 7.146061123e+01 9.5e-16 0.06
17 1.3e-10 3.2e-15 1.4e-16 1.00e+00 7.145990785e+01 7.145990903e+01 6.2e-17 0.06
18 4.8e-12 8.9e-15 1.3e-18 1.00e+00 7.145986535e+01 7.145986540e+01 2.7e-18 0.06
Optimizer terminated. Time: 0.08

Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: 7.1459509523e+01 nrm: 2e+06 Viol. con: 2e-04 var: 0e+00 cones: 0e+00
Dual. obj: 7.1459509574e+01 nrm: 1e+00 Viol. con: 0e+00 var: 1e-09 cones: 0e+00
Optimizer summary
Optimizer - time: 0.08
Interior-point - iterations : 18 time: 0.06
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00

Status: Solved
Optimal value (cvx_optval): +189.852

iteration =
2

Calling Mosek 9.1.9: 470 variables, 248 equality constraints

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:34:40)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86

Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 248
Cones : 102
Scalar variables : 470
Matrix variables : 0
Integer variables : 0

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 42
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 2 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.03
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 248
Cones : 102
Scalar variables : 470
Matrix variables : 0
Integer variables : 0

Optimizer - threads : 2
Optimizer - solved problem : the primal
Optimizer - Constraints : 205
Optimizer - Cones : 102
Optimizer - Scalar variables : 388 conic : 366
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 1397 after factor : 1748
Factor - dense dim. : 0 flops : 2.27e+04
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 2.0e+03 1.0e+00 2.1e+03 0.00e+00 6.149315915e-04 -2.099999713e+03 1.0e+00 0.05
1 3.0e+02 1.5e-01 8.2e+02 -1.00e+00 5.578739084e+00 -2.086541653e+03 1.5e-01 0.06
2 6.6e+01 3.3e-02 3.8e+02 -9.98e-01 2.908462464e+01 -2.034732003e+03 3.3e-02 0.06
3 1.2e+01 6.0e-03 1.6e+02 -9.95e-01 1.624823363e+02 -1.752681701e+03 6.0e-03 0.06
4 2.3e+00 1.2e-03 6.9e+01 -9.85e-01 8.322187505e+02 -3.718463807e+02 1.2e-03 0.06
5 5.6e-01 2.8e-04 3.3e+01 -9.57e-01 3.226858533e+03 4.440189458e+03 2.8e-04 0.06
6 1.8e-01 8.9e-05 1.7e+01 -9.03e-01 9.127685703e+03 1.595112398e+04 8.9e-05 0.08
7 4.2e-02 2.1e-05 7.0e+00 -8.12e-01 2.840450236e+04 5.199085294e+04 2.1e-05 0.08
8 2.5e-02 1.3e-05 4.8e+00 -5.92e-01 3.936001936e+04 7.072424060e+04 1.3e-05 0.08
9 5.5e-03 2.7e-06 1.2e+00 -4.39e-01 6.856153810e+04 1.141511270e+05 2.7e-06 0.08
10 1.0e-03 5.1e-07 1.2e-01 2.95e-01 3.024872377e+04 4.317269229e+04 5.1e-07 0.08
11 2.8e-05 1.4e-08 5.1e-04 8.87e-01 1.156399035e+03 1.457479462e+03 1.4e-08 0.08
12 4.0e-07 2.0e-10 8.5e-07 1.00e+00 8.749250848e+01 9.155818043e+01 2.0e-10 0.08
13 5.9e-08 2.9e-11 5.0e-08 1.03e+00 8.043390130e+01 8.108946544e+01 2.9e-11 0.08
14 7.2e-09 3.6e-12 2.0e-09 1.07e+00 7.396639870e+01 7.403390223e+01 3.6e-12 0.09
15 3.3e-10 1.6e-13 1.9e-11 1.04e+00 7.127437279e+01 7.127733378e+01 1.6e-13 0.09
16 1.3e-11 4.6e-15 8.2e-14 1.00e+00 7.115793629e+01 7.115801530e+01 4.4e-15 0.09
17 8.6e-11 1.1e-15 1.1e-15 1.00e+00 7.115517009e+01 7.115517456e+01 2.5e-16 0.09
18 1.2e-10 4.6e-15 1.3e-17 1.00e+00 7.115502559e+01 7.115502581e+01 1.3e-17 0.09
Optimizer terminated. Time: 0.09

Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: 7.1154738133e+01 nrm: 2e+06 Viol. con: 7e-03 var: 0e+00 cones: 0e+00
Dual. obj: 7.1154738362e+01 nrm: 1e+00 Viol. con: 0e+00 var: 6e-10 cones: 0e+00
Optimizer summary
Optimizer - time: 0.09
Interior-point - iterations : 18 time: 0.09
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00

Status: Solved
Optimal value (cvx_optval): +189.889

iteration =
3

Calling Mosek 9.1.9: 470 variables, 248 equality constraints

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:34:40)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86

Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 248
Cones : 102
Scalar variables : 470
Matrix variables : 0
Integer variables : 0

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 42
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 2 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.00
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 248
Cones : 102
Scalar variables : 470
Matrix variables : 0
Integer variables : 0

Optimizer - threads : 2
Optimizer - solved problem : the primal
Optimizer - Constraints : 205
Optimizer - Cones : 102
Optimizer - Scalar variables : 388 conic : 366
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 1397 after factor : 1748
Factor - dense dim. : 0 flops : 2.27e+04
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 2.0e+03 1.0e+00 2.1e+03 0.00e+00 6.034685426e-04 -2.099999718e+03 1.0e+00 0.01
1 3.1e+02 1.5e-01 8.2e+02 -1.00e+00 5.563626880e+00 -2.086577487e+03 1.5e-01 0.03
2 6.7e+01 3.3e-02 3.8e+02 -9.98e-01 2.897701718e+01 -2.034971896e+03 3.3e-02 0.03
3 1.2e+01 6.2e-03 1.6e+02 -9.95e-01 1.585949483e+02 -1.760882199e+03 6.2e-03 0.03
4 2.4e+00 1.2e-03 7.0e+01 -9.86e-01 8.132020523e+02 -4.105990671e+02 1.2e-03 0.03
5 5.7e-01 2.9e-04 3.3e+01 -9.58e-01 3.154699983e+03 4.296610261e+03 2.9e-04 0.03
6 1.8e-01 9.1e-05 1.8e+01 -9.05e-01 8.883680222e+03 1.547918440e+04 9.1e-05 0.03
7 4.3e-02 2.2e-05 7.2e+00 -8.16e-01 2.784511139e+04 5.098137811e+04 2.2e-05 0.05
8 2.6e-02 1.3e-05 4.9e+00 -5.98e-01 3.877965743e+04 6.973171342e+04 1.3e-05 0.05
9 5.6e-03 2.8e-06 1.3e+00 -4.47e-01 6.838893524e+04 1.141292424e+05 2.8e-06 0.05
10 1.1e-03 5.3e-07 1.3e-01 2.76e-01 3.148937639e+04 4.510837968e+04 5.3e-07 0.05
11 3.1e-05 1.6e-08 6.1e-04 8.81e-01 1.285102154e+03 1.625264518e+03 1.6e-08 0.05
12 4.1e-07 2.1e-10 9.0e-07 1.00e+00 8.747601404e+01 9.173761053e+01 2.1e-10 0.05
13 5.8e-08 2.9e-11 5.0e-08 1.03e+00 8.011079676e+01 8.076895627e+01 2.9e-11 0.05
14 7.2e-09 3.6e-12 2.0e-09 1.07e+00 7.369814608e+01 7.376589641e+01 3.6e-12 0.05
15 3.4e-10 1.7e-13 2.0e-11 1.05e+00 7.100523228e+01 7.100832256e+01 1.7e-13 0.05
16 1.5e-11 4.7e-15 9.0e-14 1.00e+00 7.088387584e+01 7.088396001e+01 4.6e-15 0.06
17 3.5e-11 1.4e-15 1.2e-15 1.00e+00 7.088092648e+01 7.088093121e+01 2.6e-16 0.06
18 1.4e-10 4.0e-15 1.3e-17 1.00e+00 7.088077338e+01 7.088077361e+01 1.3e-17 0.06
Optimizer terminated. Time: 0.06

Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: 7.0880491657e+01 nrm: 2e+06 Viol. con: 7e-03 var: 0e+00 cones: 0e+00
Dual. obj: 7.0880491890e+01 nrm: 1e+00 Viol. con: 0e+00 var: 3e-10 cones: 0e+00
Optimizer summary
Optimizer - time: 0.06
Interior-point - iterations : 18 time: 0.06
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00

Status: Solved
Optimal value (cvx_optval): +189.889

This is the optimized variable：
image
when I use sedumi:
it stopped with NAN.

3

I’d appreciate it if you could give me some advice

4

The argmax to your problem is not unique. That can be the case for an individual convex optimization problem. When run as part of an iterative SCA algorithm, you could be lucky that convergence to the same optimal objective value occurs using different solvers. That may or may not be the case if you change the starting values.

5

thank you very much,I have changged the starting values,it convergence to the same optimal objective value , I…,okay,there may be some problem with my model,The results are not consistent with the theoretical derivation，I will channged my model,thanks for your time!