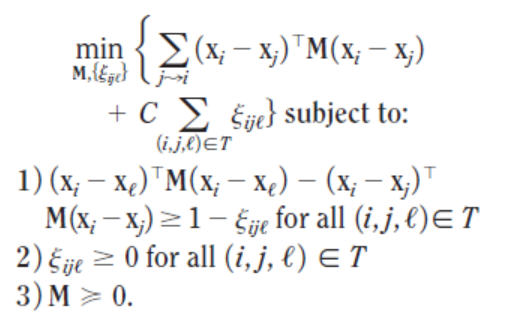Solving KNN Optimization in CVX

1

I am attempting to solve the following convex optimization problem in CVX for variables M and E:

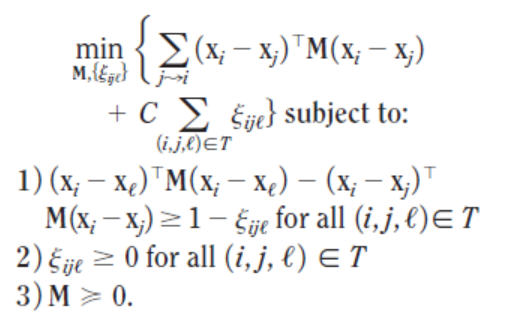
Maths

As you can see, the objective function requires the use of two summations: one over all i, and one over all j.

Unfortunately, I haven’t been able to find any documentation anywhere that discusses how/if it is possible to use such notation within a CVX block.

Is this even possible?

2

You can avoid using for loops in the objective by observing that

\sum_{j\to i}(x_i-x_j)^TM(x_i-x_j)=\text{trace}(DM)

where

D=\sum_{j\to i}(x_i-x_j)(x_i-x_j)^T

is a fixed matrix defined outside of the call to CVX. You can do a similar thing for the slack-variables term, defining a binary matrix/3d-array.

(Another approach is to put it in epigraph form, which would shift the for loops from the objective to the constraints.)

3

Thanks, Bien. That’s actually what I ended up doing. Great minds think alike!