I guess some elements of A(k, : ) are <= 0 but some are not. You can read the error that implied something like that. Maybe you can paste your complete code on here next time if convenient.
for K = 5
T = 70; N = 140; delta = T/N;
w = [50,150,200,450,475;
125,100,350,300,450];
for c = 1:K
data(1,c) = 200; % 初始化需要传输的数据量(bit)
end
for c = 1:K
data2(1,c) = 2^200; % 初始化需要传输的数据量(bit)
end
for c = 1:K
energy(1,c) = 0.0001; % 初始化需要传输的数据量(bit)
end
for c = 1:2
for n = 1:N
Q_int(c,n) = 500/N*n; % 初始化无人机路径
end
end
for k = 1:K
for n = 1:N
L_int(k,n) =1; % 初始化无人机路径
end
end
for a = 1:K
for n = 1:N
P_int(a,n) = 4; % 初始化发射功率
end
end
N_0 = -100; H = 20;
% 噪声功率(单位转换)
dBm = N_0 ;
sigma = power(10, dBm/10 ) /1000 ; % 单位 w
% Unit conversion of beta_0
beta = 1000 ;
% variables
%T = 75; N = 140;
delta = T/N;
% the square of distance between UAV and kth GN in time slot n
for k = 1:K
for n = 1:N
d(k,n) = norm( Q_int(:,n) - w(:,k) );
SoD(k,n) = power( d(k,n), 2 ) + power(H,2);
phi(k,n) = beta/sigma/SoD(k,n); % 计算 phi_k[n]
changshu1(k,n) = log2(L_int(k,n)+phi(k,n).*P_int(k,n))
changshu2(k,n) = beta*P_int(k,n)/SoD(k,n)
end
end
% 使用CVX工具包求解调度参数
cvx_begin
% cvx_solver mosek
variables A(K,N)
maximize (delta*sum( A(k,:).*changshu1(k, ))
))
subject to
% constraint 21
for k = 1:K
delta*sum( A(k,:).*changshu1(k,:) ) >= data(k);
end
for k = 1:K
delta*sum( (L_int(k,:)-A(k,:)).*changshu2(k,:) ) >= energy(k);
end
%13 14
for n = 1:N
sum(A(:,n)) <= 1;
end
% 19 20
for k = 1:K
for n = 1:N
A(k,n) >= 0;
end
end
cvx_end
E_1 = delta*sum( A(k,:).*changshu1(k, );
);
cvx_begin
% cvx_solver mosek
variables P(K,N)
maximize (delta*(sum( A(k,:).*(log(phi(k,:).P(k,:)+L_int(k,:)) -0.2(2^(sum(P(k,:))))))))
subject to
% constraint 21
for k = 1:K
delta*(sum( A(k,:).*(log(phi(k,:).*P(k,:)+L_int(k,:))))) >= data(k) ;
end
%13 14
for k = 1:K
beta* delta*sum( (L_int(k,:)-A(k,:))/SoD(k,:).*P(k,:) ) >= energy(k);
end
% 19 20
for k = 1:K
for n = 1:N
0 <= P(k,n) <=20;
end
end
for n = 1:N
P(1,n)== P(2,n) == P(3,n)== P(4,n) == P(5,n);
end
cvx_end
Thanks, you give me a great help.
I show my code,please check my code,thanks.
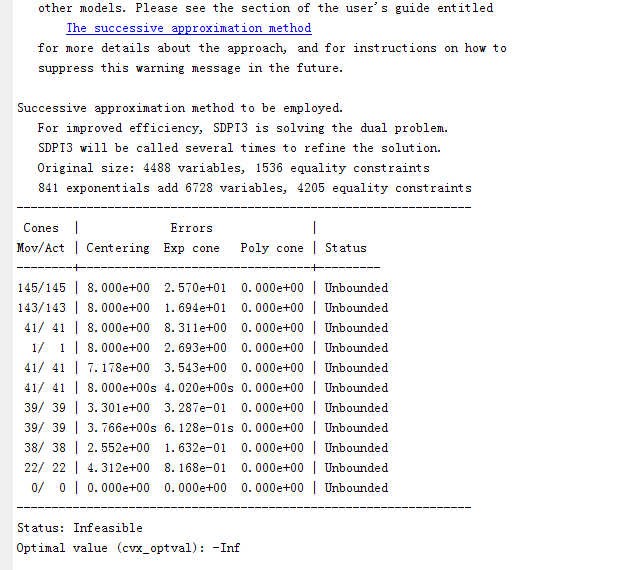
The output said it’s infeasible. Maybe it is infeasible.
It seems you use cvxquad. I doubt that is needed and it is better to use Mosek without cvxquad as described in the 2020 update on:
The output shows that CVX’s Successive Approximation method was used with SDPT3 as solver. cvx_solver mosek is commented out.
But as @Erling wrote, it would be better to use Mosek (with CVX 2.2) thereby avoiding CVX’s Successive Approximation method, and getting a more robust and reliable solution.
As for infeasible problems, follow the advice, except for section 1, in https://yalmip.github.io/debugginginfeasible, which also applies to CVX.
I use MAC
I have been unable to install Mosek properly
I have an official license ,but i don’t know how to use it.
Do you have any experience in this field
This
including the “testting” and “troubleshooting” sections should help you get started with Mosek.
Also, make sure you are using CVX 2.2
I have tried mosek, but it still show infeasible
do you have other advices?
I showed my code.
do you kwon why it is infeasible.
Can you post the full log output from MOSEK. Or, alternatively, a fully reproducible code, completely preformatted, so that it can be copy-pasted and run without effort. (At the moment it is a bit of work to convert your code into something runnable.)
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: 2.0514922393e+10 nrm: 2e+08 Viol. con: 6e-03 var: 0e+00
Dual. obj: 2.0514922394e+10 nrm: 2e+03 Viol. con: 0e+00 var: 7e-08
Basic solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: 2.0514922393e+10 nrm: 2e+08 Viol. con: 6e-08 var: 0e+00
Dual. obj: 2.0514922393e+10 nrm: 2e+03 Viol. con: 0e+00 var: 6e-14
Optimizer summary
Optimizer - time: 1.09
Interior-point - iterations : 16 time: 0.94
Basis identification - time: 0.08
Primal - iterations : 0 time: 0.01
Dual - iterations : 0 time: 0.02
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
Status: Solved
Optimal value (cvx_optval): +2.05149e+10
CVX Warning:
Models involving “log” or other functions in the log, exp, and entropy
family are solved using an experimental successive approximation method.
This method is slower and less reliable than the method CVX employs for
other models. Please see the section of the user’s guide entitled
The successive approximation method
for more details about the approach, and for instructions on how to
suppress this warning message in the future.
Calling Mosek 9.1.9: 1427 variables, 145 equality constraints
For improved efficiency, Mosek is solving the dual problem.
MOSEK Version 9.1.9 (Build date: 2019-11-21 11:32:15)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: MACOSX/64-X86
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (3) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (4) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (5) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (6) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (7) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (8) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (1407) of matrix ‘A’.
MOSEK warning 710: #1 (nearly) zero elements are specified in sparse col ‘’ (1408) of matrix ‘A’.
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 145
Cones : 6
Scalar variables : 1427
Matrix variables : 0
Integer variables : 0
Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 1 time : 0.00
Lin. dep. - tries : 1 time : 0.02
Lin. dep. - number : 0
Presolve terminated. Time: 0.08
Optimizer terminated. Time: 0.27
Interior-point solution summary
Problem status : DUAL_INFEASIBLE
Solution status : DUAL_INFEASIBLE_CER
Primal. obj: -7.8460433661e+02 nrm: 3e+11 Viol. con: 0e+00 var: 0e+00 cones: 7e-15
Optimizer summary
Optimizer - time: 0.27
Interior-point - iterations : 0 time: 0.13
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
Status: Infeasible
Optimal value (cvx_optval): -Inf
I don’t know it is what you want, if you want more information, please tell me.
Thanks for your help.
You are showing 2 different Mosek outputs. What is the difference between the problems you’re solving?
The first was solved to optimality, but the optimal objective value of 2e10 is indicative of very bad numerical scaling.
In the second, Mosek issues warning about nearly zero elements in the input data. Mosek reports dual infeasibility, but it was provided the dual, so I think that should correspond to primal unbounded, yet CVX reports it as (primal( infeasible. This seems to be the same thing as happened in How to minimize the largest singular value of the matrix , So I don’t know whether this is really infeasible or unbounded. Nevertheless, I suggest you improve scaling (by changing units) so that all input data is within s small number of orders of magnitude of 1, then re-run it and see what Mosek and CvX report.
sorry, i can not understand changing units
i do not know how to change units. can you tell me more details.
A variable has a unit e.g it can be meters/second or km/hour or something else. So you should chose decent units.
PS. It seems you still use CVXQUAD because your last logout has:
CVX Warning:
Models involving “log” or other functions in the log, exp, and entropy
family are solved using an experimental successive approximation method.
This method is slower and less reliable than the method CVX employs for
other models. Please see the section of the user’s guide entitled
The successive approximation method
for more details about the approach, and for instructions on how to
suppress this warning message in the future.

cvx_begin
cvx_solver mosek
variables P(K,N)
maximize (delta*(sum(A(k,:).*(log(phi(k,:). P(k,:)+L_int(k,:)) -0.2 (2^(sum(P(k,:))))))))
subject to
% constraint 21
for k = 1:K
delta*(sum( A(k,:).*(log(phi(k,:).*P(k,:)+L_int(k,:))))) >= data(k) ;
end
for k = 1:K
beta* delta*sum( (L_int(k,:)-A(k,:))/SoD(k,:).*P(k, ) >= energy(k);
) >= energy(k);
end
for k = 1:K
for n = 1:N
0 <= P(k,n) <=20;
end
end
cvx_end
i find if i delete subject delta*(sum( A(k,:).*(log(phi(k,:).*P(k,:)+L_int(k,:))))) >= data(k) ;
cvx can solve it
i show my Original optimization problem,can you help me if code is right?
I suggest you make your complete code available including the data so we can reproduce the issue. If you do then please remove all Chinese letters from code.
This
CVX Warning:
Models involving “log” or other functions in the log, exp, and entropy
family are solved using an experimental successive approximation method.
This method is slower and less reliable than the method CVX employs for
other models. Please see the section of the user’s guide entitled
The successive approximation method
for more details about the approach, and for instructions on how to
suppress this warning message in the future.
is not indicative of what method CVX actually used to solve the problem. It is always printed, which is a “bug” in CVX, whether the Successive Approximation method, CVXQUAD, or Mosek native exponential cone is used. In this case, based on the output, Mosek native exponential cone was apparently used. The only way to know for sure whether CVXQUAD was (also) used is to see whether there are any Pade Approximant messages prior to the beginning of the solver output.