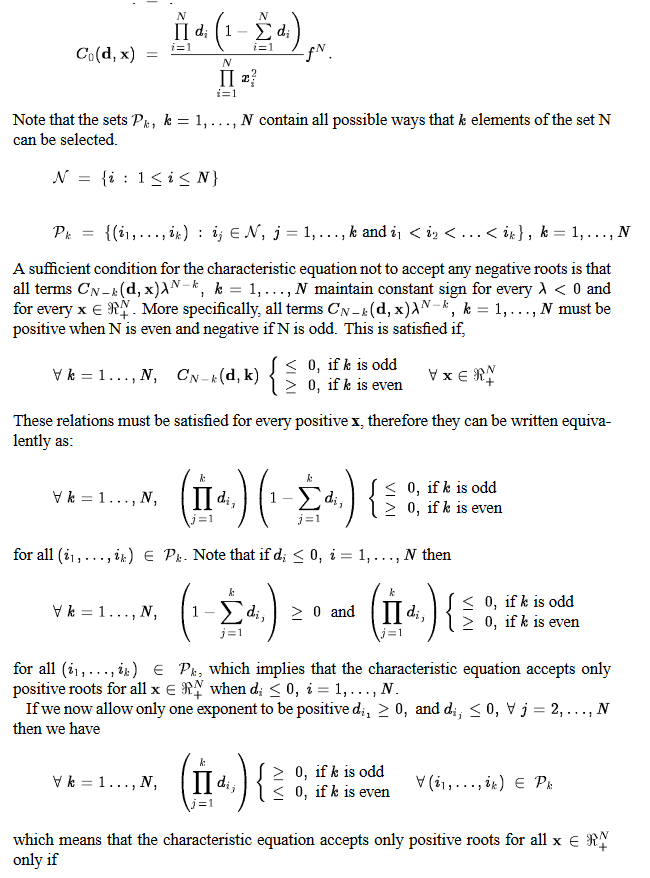min 0.5*( x(6)^2.5x(7)^(-0.5) )+0.4( x(8)^2.7x(7)^(-0.6) )
s.t. 0.5(x(1)^(-0.1))(x(2)^(-0.2))(x(3)^(-0.3))(x(4)^(-0.1))(x(5)^(-0.2))-0.6*(x(1)^(0.01))(x(2)^(0.03))(x(3)^(0.02))(x(4)^(0.05))(x(5)^(0.01))<=0.5
0<=x(i)<=2,i=1,2,3,4,5
1<=x(6)<=11
1<=x(7)<=12
1<=x(8)<=13Have you proven that this is a convex optimization problem. Why isn’t CVX accepting my model? READ THIS FIRST!
I think your objective function is convex. I’ll let you fix up the first constraint with missing symbols, make sure parentheses are correct, etc. Please prove it is convex.
I’m sorry, there was a sign error in the question, and the following one is correct
min 0.5*( (x(6)^2.5)(x(7)^(-0.5)) )+0.4(( x(8)^2.7)(x(7)^(-0.6)) )
s.t. 0.5(x(1)^(-0.1))(x(2)^(-0.2))(x(3)^(-0.3))(x(4)^(-0.1))(x(5)^(-0.2))-0.6*(x(1)^(0.01))(x(2)^(0.03))(x(3)^(0.02))(x(4)^(0.05))(x(5)^(0.01))<=0.5
0<=x(i)<=2,i=1,2,3,4,5
1<=x(6)<=11
1<=x(7)<=12
1<=x(8)<=13
Inspired by theorems 2.1 and 2.2 in a paper, I constructed constraints and objective functions, but I don’t know how to prove that my constraint function is convex function, which is difficult for me。
This paper is http://users.abo.fi/twesterl/selected-publications/9.%20OMS-AL-TW-2009.pdf
Per the link I provided, it’s your obligation to prove convexity. If you have done that, then perhaps readers can offer reformulation tips.

What is f? That doesn’t appear to be left-hand side of the first constraint, whose convexity you need to prove, and which remains very much in doubt, to put it mildly.
Can you please write out clearly what your constraint is? Is that constraint convex?
My constraint is f(x)+g(x)<=0.5, I have proved that both f(x) and g(x) are convex,so I think the constraint
f(x)+g(x)<=0.5 is also convex.
Formulate it in CVX using gp mode. Form f, and see what type of objects CVX says it is (just enter f on the command line) Similarly with g. if f and g are both generalized posynomials, then f + g <= constant should be accepted by CVX in gp mode. http://cvxr.com/cvx/doc/gp.html#
Thank you very much. In the constraint f(x)+g(x)<=0.5, g(x) is a negative term, and I need to move g(x) to the right of the inequality if I use gp mode in CVX , so that I get the constraint f(x)<=-g(x)+0.5, however, g(x)+0.5 is not a monomial,can I still use gp mode in such a situation?
I keep losing track of what you are doing, with minus signs coming and going, inside g, in front of g, whatever, so I really don’t know what your constraint is… So I don’t know whether the 2nd term of your left-hand side is going the correct direction. Of course f(x) + g(x) <= 0.5 is not the same as f(x) <= g(x) + 0.5 . Please refer to my previous post and study the Geometric Programming (gp) chapter linked there.
I’m sorry, I may not have made my question clear. I mean, both f(x) and g(x) is convex, therofore the constraint f(x)+g(x)<=0.5 is convex, f(x) is a positive monomial, while g(x) is a negative monomial , how to code with cvx to solve the problem?
You’re claiming a negative monomial is convex? That sounds dubious to me. if somehow that is true, i don;t know how to handle it in CVX, and will have to defer to someone else.
Yes. I have proved that g(x) is convex, which is a negative monomial .
Dear Mark, thank you very much for your help. In the past few days, I have tried other ways to solve this problem, but there is still no progress. This problem is very important to me. Can you help me find a way to solve it? I will wait for your reply with anxiety and expectation.
If you can not produce a formulation acceptable to CVX, you can use another tool whch can handle “general” nonlinear models.