How to make a convex problem be accepted by CVX?

1

Recently, I meet a question as follows:

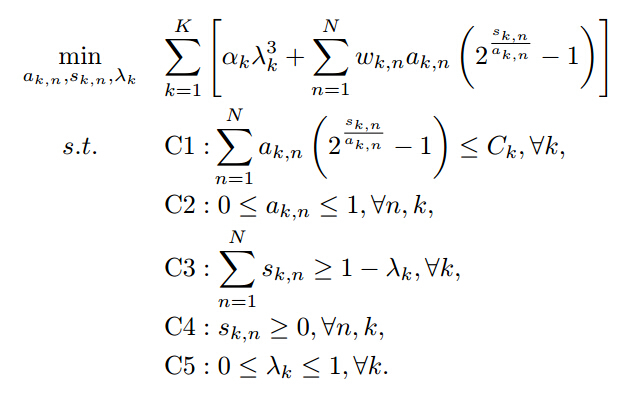
In this convex problem, a_k,n and s_k,n is K*N matrix, while \lambda_k is a vector. I have proved this problem to be a convex one. Now, the key issue is how to let the convex funtion f(x,y)=x(2^(y/x)-1) be accepted by CVX. Hope for your help and thanks very much.

2

Your f(x,y) is not convex when x < 0. Even though you have another constraint that restricts this x to be >= 0, this can be a difficult type of situation for CVX to handle. However, I am not saying that it can not be done.

3

I doubt CVX will be able to handle this one, sorry.

4

This is very similar to a problem by the same OP which was solved by @Bien at Let this function be supported by CVX by reparameterizing the key variables in terms of logs… In the previous problem, the OP did not provide the full optimization problem to Bien before his solution, which wound up not allowing its use.

I think Bien’s approach would work quite nicely in this problem if there were no “- 1” term. I don’t see how to deal with that in a way which would be acceptable to CVX.