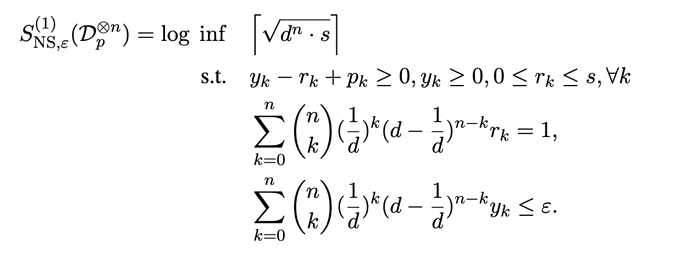I have to solve the following linear program in CVX. I choose d=2.
I have written the following LP as a start but it has two issues
n = 1000;
eps = 0.001;
cvx_begin
variable y(n)
variable r(n)
variable p(n)
variable s
minimize(s)
subject to
y >= 0;
y - r + p >= 0;
r >= 0;
for i=1:n
r(i) <= s;
end
ones(1,n)*r == 1;
ones(1,n)*y <= eps;
cvx_end
-
I should be minimizing sqrt(d^n * s) but since s is nonnegative (from the constraints), I just minimized s directly. Does this make sense?
-
I don’t know how to encode summation constraints. I need to replace the lines
ones(1,n)*r == 1;
ones(1,n)*y <= eps;
with the correct constraint which is the one involving some combinatorial prefactors and then a sum over r(k) and y(k). How should one encode such a sum constraint? This is my second attempt below but gives an error “Unrecognized field name “sol”.”
n = 1000;
d = 2;
eps = 1e-5;
for i = 1:n
c(i) = nchoosek(n, (i-1))*(1/d)^(i-1)*(d - 1/d)^(n-i+1);
end
cvx_begin
variable y(n)
variable r(n)
variable p(n)
variable s
minimize(s)
subject to
y >= 0;
y - r + p >= 0;
r >= 0;
for i=1:n
r(i) <= s;
end
c*r == 1;
c*y <= eps;
cvx_end
For n=1000 the computation of your c coefficients is so inaccurate that it produces some humonguous values. Are you not getting a ton of warnings related to calling nchoosek ? You will need to compute them in some more clever way that does not lead to overflows.
That’s why for n=1000 Mosek says
Mosek error: MSK_RES_ERR_HUGE_AIJ (A numerically huge value is specified for an element in A.)
------------------------------------------------------------
Status: Error
Optimal value (cvx_optval): NaN
Reference to non-existent field 'sol'.
For n=10 it solves nicely.
1 Like
Ah thanks! Somehow the nchoosek warnings were being suppressed but now I see the issue is not CVX
Hi Michal,
Would you have any suggestions on how to cleverly compute the coefficients to avoid overflows in such a case? I have a different (simpler) linear program where I run into the same issue which I include here
clear all
cvx_solver mosek
N = 50;
eps = 0.01;
delta = 0.2;
for n=1:N
for i = 1:n+1
w(i, 1) = delta^(i-1)*(1-delta)^(n-i+1);
nck(1,i) = nchoosek(n, i-1);
end
cvx_begin
variable til_w(n+1)
variable p(n+1)
variable zeta
minimize(zeta)
subject to
p >= 0;
nck*p <= eps;
p - til_w + w >= 0;
nck*til_w ==1;
til_w >= 0;
til_w <= zeta*ones(n+1, 1);
cvx_end
zeta_opt(n) = zeta;
n_copies(n) = n;
obj(n) = 1 + 1/n*log(zeta)/log(2);
end
I get warnings about nchoosek again but it’s not clear what is the best way to avoid this issue. Thank you.
Your constraint nck*til_w ==1; will have coefficient span between 1 and 2^n (roughly asymptotically) while looking at the rest of the problem it seems like you are expecting the variable til_w in the solution to have values of order similar to w, that is to say 1/2^n when \delta=1/2. There is no way to make this floating-point meaningful for n=50.
I see. Somehow, the authors of https://arxiv.org/pdf/1807.05354.pdf manage to solve a similar LP by symmetrizing the SDP in my original post for n=10,000 (see Fig. 2).
Of course, this is not necessarily a CVX question anymore but curious how they managed it since it appears it can be done somehow. Thanks anyway for your comments!
I agree both that the question is interesting and not related to CVX :). Maybe asking the authors can help.
1 Like