How to deal with {real affine} - {invalid}

[HYZ]

N=128;
theta1=1e-3;
P_avg=1;
belta0=1e-3;
alpha=2.8;
S=[20,30,46,56,94,100,112,162,178,200;10,28,0,24,168,200,176,0,40,6];
H=50;
V_max=40;
T=20;
delta_t=T/N;
q0=[0;0];
qF=[200;200];
load(‘PerformanceComparison_Constrained_Main0206.mat’,‘qj_initial’,‘P_DatarateMax_Givenpath’,‘a_DatarateMax_Givenpath’)
MAX_ITR=2 ; %maximum iteration number
itr_cur=1;
eps=0.01;
Datarate_max=0;
optval_max=9;
old_optval=0;
new_optval=9;
qj=qj_initial;
Pj=Pj_initial;%Transmit power
aj=aj_initial;
Datarate_seq_Givenpower=[];
while itr_cur>=1
while (itr_cur>=MAX_ITR)||((abs(new_optval-old_optval))/optval_max<eps)
break;
end
old_optval=Datarate_max;

cvx_begin
cvx_solver sedumi

% cvx_quiet(true);
variable q(2,N+1); %the trajectory
variable A(1,N+1);
variable a(10,N+1);

maximize (sum(log(1+A./theta1))./(log(2)*N))
subject to

for n=1:N+1
    ajn=aj(:,n);
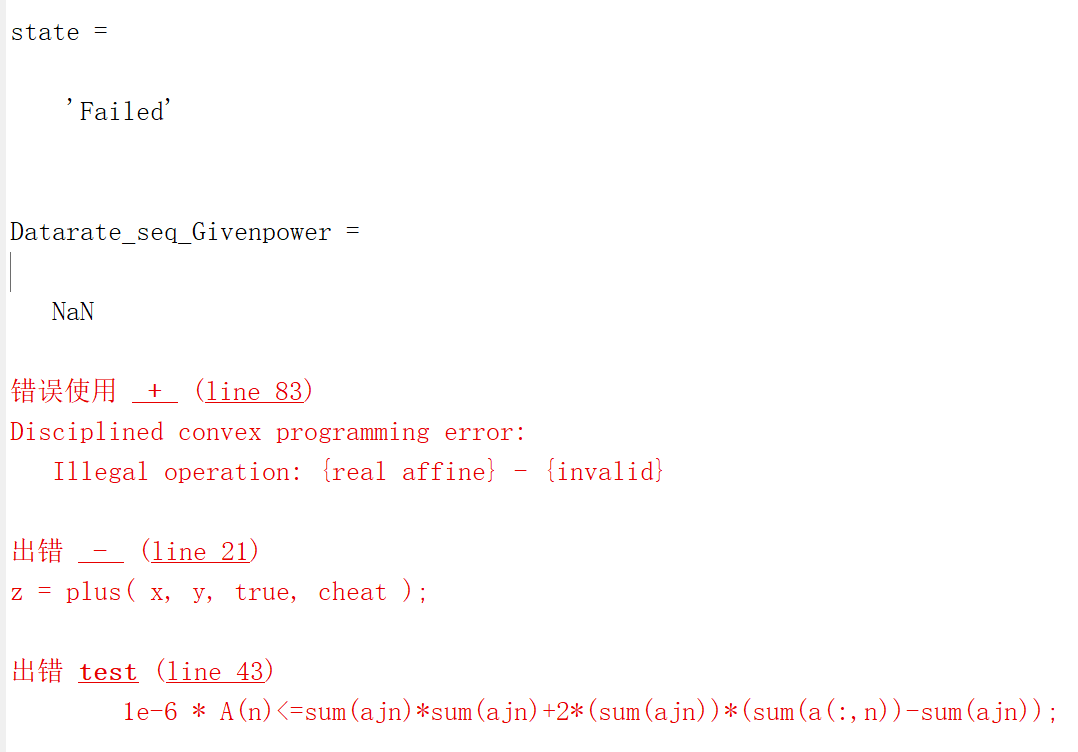
    1e-6 * A(n)<=sum(ajn)*sum(ajn)+2*(sum(ajn))*(sum(a(:,n))-sum(ajn));
end

for k=1:10
    for n=1:N+1
        qjn=qj(:,n);
        1e-3 * a(k,n)<=1e-3 * sqrt(Pj(k,n)*belta0)*(((norms(qjn-S(:,k))).^2+H^2)^(-alpha/4)-alpha*((pow_pos(norms(q(:,n)-S(:,k)),2))-(norms(qjn-S(:,k))).^2)*(4*((norms(qjn-S(:,k))).^2+H^2)^(-alpha/4-1)));
    end
end

for n=2:N+1
    (pow_pos(norms(q(:,n)-q(:,n-1)),2))<=V_max^2*delta_t^2;
end
     
if ~isempty(q0)
    q(:,1)==q0;
end

if ~isempty(qF)
    qF==q(:,N+1);
end

cvx_end

Datarate_max=cvx_optval
new_optval=Datarate_max;
state = cvx_status

Datarate_seq_Givenpower =[Datarate_seq_Givenpower [Datarate_max]]

itr_cur=itr_cur+1;

qj=q;
aj=a;

end

q_conv_Givenpower=q;
A_conv_Givenpower=A;
a_conv_Givenpower=a;

[Mark_L_Stone]

What's wrong with cvx?

Elaborating on @jackfsuia 's answer, if one iteration of CVX fails due to being infeasible or solver numerical difficulty, the variable values are populated with NaN, which are then fed in as input data to the next iteration. CVX considers NaN input data to be invalid, hence the error message. You should ask not what is wrong with CVX, but what is wrong with crude, unsafeguarded SCA.

https://twitter.com/themarklstone/status/1586795881168265216

[HYZ]

Thank you very much for your reply! This is the problem I encountered when reproducing the paper. The SCA method is used in the paper, which shows that the problem can be solved by the SCA method . I would like to ask what should I do for the current problem.

[Mark_L_Stone]

Does the paper include the code? Maybe their code is Better than yours. Maybe the paper uses a different starting value? Or a different solver? Is the paper’s input data the same? The authors of the paper might have used some tricks to get it to work - it might have failed many times before they finally succeeded.

[HYZ]

The corresponding code is not given in the article, but it is also solved by CVX. I would like to ask what are some tricks you said.

[Mark_L_Stone]

Ask the authors for their CVX code, and if the solver is mot specified, ask them what solver and solver version they used. Ask them what starting value they used. If your input data is different than theirs, their stating value might not help you.