Hello everyone! I’m new to the forum and I haven’t been familiar with DCP ruleset. Could someone give me some examples to solve these problems below using DCP ruleset properly? 
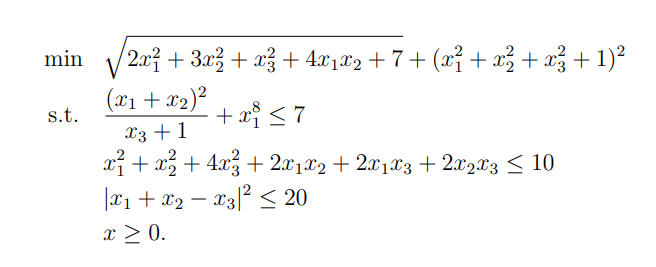
You need to formulate the first term of the objective as the norm of something. The 2nd term of the objective function can be entered “as is”.
.
The first term in the LHS of the 1st constraint can be formulated using
quad_over_lin, The 2nd term can be entered as is.
The LHS of the 2nd constraint needs to be formulated as a convex quadratic form.
The 3rd constraint can be entered almost as is, but using square_pos for the squaring. Or better yet, don’t square the LHS, and take the sqrt of the RHS.
First term of objective function:
norm([sqrtm([2 2 0;2 3 0;0 0 1])*x;sqrt(7)])
(if you want to learn something, try formulating this using chol instead of sqrtm).
LHS of 2nd constraint
x'*[1 1 1;1 1 1;1 1 4]*x <= 10
or equivalently
quad_form(x, [1 1 1;1 1 1;1 1 4]) <= 10
I’ll leave you to implement the rest, so that you will learn something. But first, if you have not already, read the CVX Users’ Guide
If you want to further improve your understanding and facility with CVX, reformulate the 2nd constraint as a Second Order Cone constraint, i.e., norm(first_something) <= second_something , where both instances of something are affine (which includes a constant as special case). Hint: look at the “trick” I used for the first term of the objective function
Thank you very much!
Maybe something like
0.5 x^T Q x + a^T x + b \leq t, t\geq 0,
and
\sqrt{t} \leq s
can work under suitable assumptions e.g. x\geq 0 and Q positive semi-definite.
@Erling But \sqrt{t} \leq s is non-convex.
However, I think, but am not sure, that
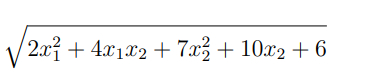
is convex. Perhaps another Erling’s challenge candidate?
Yes, I am wrong. sqrt(t) is concave and not convex which I need. Pretty stupid of me.