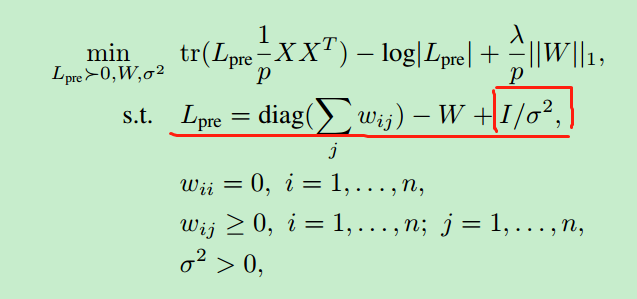Hello, everyone, when I try to solve the following problems:
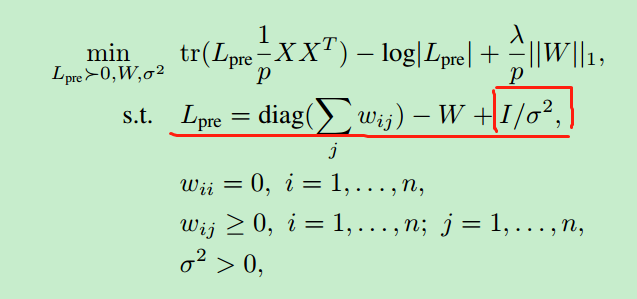
For the first constraint (I is an identity matrix) , I try to code as
L == diag(sum(W,2))- W + 1/(sigma)*I
However, the following error occurs
Disciplined convex programming error:
Cannot perform the operation: {positive constant} ./ {real affine}
because of 1/(sigma)*I.
To avoid this error , I try to use inv_pos replacing 1/(sigma), i.e.,
L == diag(sum(W,2))-W + inv_pos(sigma)*I
The following error then occurs
Disciplined convex programming error:
Invalid constraint: {real affine} == {convex}
Because L, diag(sum(W,2)) and W are all real affline experssion while inv_pos(sigma)*I is convex expression. This mismatch causes the error.
My quesition is how I can avoid this error? I read the DCP ruleset and have not found the solution.
Thank you very much if anyone can answer my quesition!
L_{pre} = ... isn’t intended to be a constraint. Rather, it defines L_{pre} for use in the intended semidedfinite constraint L_{pre} >= 0 (actually, supposed to be a strict positive definite constraint), I.e., RHS >= 0, where I have presumed sdp mode has been specified. And also specifies L_{pre} as the argument of log_det and the trace term in the objective function.
In order to make L_{pre} affine, and hence valid in CVX as a constituent of an SDP constraint or argument of log_det, 1/\sigma^2 needs to be defined as the variable, rather than \sigma or \sigma^2 That will make L_pre affine in the CVX (optimization) variables.
Make L_pre = … an expression assignment by using =, not ==, and place that prior to its use in the objective function. Then add the semidefinite constraint on L_pre, or perhaps on L_pre - small_positive_number*eye(n) in order to make it a strict positive definite constraint, if that is really required.
cvx_begin sdp
...
variable one_over_sigma_squared
L_pre = ...
minimize ...
L_pre - small_positive_number*eye(n) >= 0
one_over_sigma_squared >= 0
...