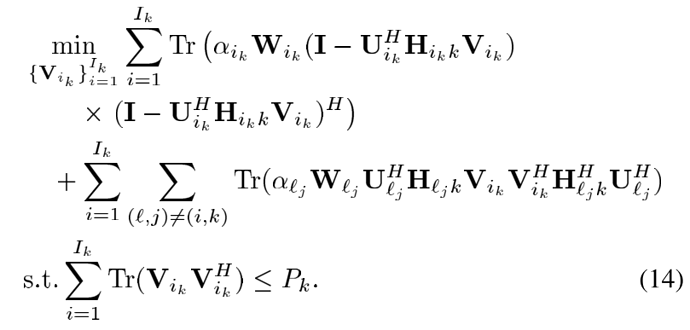Help with Invalid quadratic form(s): not a square

1

Hi, everyone.I have problem to solve the following question, which is convex.

image
image809×387 21 KB

and this is my code
cvx_clear

cvx_begin
variable v_hat(T,d,K) complex
expression E(d,d,K)
% v_hat = V;
for k = 1:K
E(:,:,k) = eye(d) - v_hat(:,:,k)’* H(:,:,k)’* U(:,:,k) - U(:,:,k)’* H(:,:,k)* v_hat(:,:,k);
E(:,:,k) = E(:,:,k) + sigma^2 * U(:,:,k)’* U(:,:,k);
for m = 1:K
E(:,:,k) = E(:,:,k) + U(:,:,k)’* H(:,:,k)* v_hat(:,:,m)* v_hat(:,:,m)’* H(:,:,k)’* U(:,:,k);
end
end
minimize (sum(weights(k) * trace(W(:,:,k) * E(:,:,k))))
subject to
norm(v_hat(:,:,:), 2) - PK <= 0;
cvx_end
V = v_hat;

error in line 86:
Disciplined convex programming error:
Invalid quadratic form(s): not a square.

I recently started to learn it, please help me

2

Reformulate trace(V*V') as square_pos(norm(V,'fro'))

The other terms can be handled presuming alpha >= 0 and W is psd.

Reformulate alpha*W*something*something' as alpha*square_pos(norm(sqrtm(W)*something,'fro')), which makes use of W = sqrtm(W)*sqrtm(W) and then rearranges using cyclic permutation invariance of trace. Or if W is strictly positive definite., that formulate cab be used, or can use alpha*square_pos(norm(chol(W)'*something,'fro')),

3

Thanks for your help. Could i still use sqrtm(W)*sqrtm(W) to replace W even if W is not positive definite?(W is a complex matrix).

4

I believe it should work if W is Hermitian semidefinite.

if it isn’t, sqrtm may not even be Hermitian, which would invalidate the reformulation in my previous post. Moreover, the objective function might not even be convex.