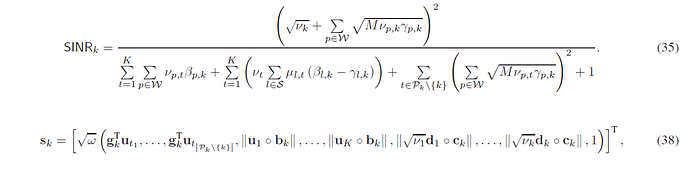The problem is that:
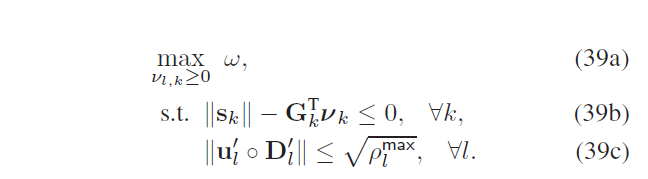
The vector sk contains :cvx convex expression (scalar),cvx zero constant expression (scalar),and cvx real affine expression (scalar).
I use this expression for constraint (39b):
norm(s_k(k,:))<=G_k(:,k).’*v_k(:,k);
however, matlab told me that
“Disciplined convex programming error:
Cannot perform the operation norm( {mixed
convex/constant/affine}, 2 )”
in my opinion, the function norm is convex, and Gk’*vk is a scalar, so the constraint (39b) is convex.
Is there anyone who can help me solve this problem? Thanks a lot.
If s_k was an affine expression then it would be fine but you seem to indicate that s_k is something more complicated than that (and you have not shown what it is).
Thank you very much for your reply. The vector s_k is a vector with 3K+1 elements. the elements 1:K are 0 or cvx real affine expression (scalar)(because pilot reuse in the communication), the elements K+1:3K are convex expression, the last element is 1;
the code is too trivial to read, but I think I can upload it below.
%% MMF Power Comtrol
wmin = 2^min(R_cf_JMRZF(n,:))-1;
wmax = 2^20 -1;
espi = min(wmin/5,0.01);
miu = zeros(Cl,K);
for l = 1:Cl
miu(l,:) = diag((selected(M,Cl,l)*pre_Ws_czf)'*(selected(M,Cl,l)*pre_Ws_czf)).';
end
g_k = zeros(Wl,K);
G_k = ones(Wl+1,K);
for l = Cl+1:L
for k = 1:K
g_k(l-Cl,k) = sqrt(M*GAMMAAN(l,k));
G_k(l-Cl+1,k) = sqrt(M*GAMMAAN(l,k));
end
end
d_k = miu.^(1/2);
c_k = zeros(Cl,k);
for l = 1:Cl
for k = 1:K
c_k(l,k) = sqrt(BETTAAN(l,k)-GAMMAAN(l,k));
end
end
b_k = zeros(Wl,K);
for l = Cl+1:L
for k = 1:K
b_k(l-Cl,k) = sqrt(BETTAAN(l,k));
end
end
D_l = ones(L,K);
for l = 1:Cl
D_l(l,:) = d_k(:,k)';
end
%cvx_solver sedumi
cvx_quiet true
while(wmax-wmin>espi)
wnext = (wmax+wmin)/2;
cvx_begin sdp
expressions u_k(Wl,K) u_s(1,K) u_l(L,K) s_k(K,3*K) v_k(Wl+1,K) summ(1,K)
variables v_zf(K,1) v_mrt(Wl,K)
u_k = v_mrt;
u_s = v_zf.';
for l = 1:Cl
for k = 1:K
u_l(l,k) = u_s(k);
end
end
for l = Cl+1:L
for k = 1:K
u_l(l,k) = u_k(l-Cl,k);
end
end
for k = 1:K
v_k(1,k) = u_s(k);
end
for l = 2:Wl+1
for k = 1:K
v_k(l,k) = u_k(l-1,k);
end
end
for k = 1:K
for t = 1:K
if t~=k
if Phii_cf(:,t)'*Phii_cf(:,k)>0.9
s_k(k,t) = g_k(:,k)'*u_k(:,t);
else
s_k(k,t) = 0;
end
else
s_k(k,t) = 0;
end
end
for t = K+1:2*K
s_k(k,t) = norm(u_k(:,t-K).*b_k(:,k));
end
for t = 2*K+1:3*K
s_k(k,t) = norm(v_zf(k)*d_k(:,t-2*K).*c_k(:,k));
end
s_k(k,3*K+1) = 1;
end
minimize(0)
subject to
for k = 1:K
v_zf(k)>=0;
wnext*norm(s_k(k,:))<=G_k(:,k).'*v_k(:,k);
end
for l = 1:L
norm(u_l(l,:).*D_l(l,:))<=sqrt(Pd);
end
for l = 1:Cl
for k = 1:K
v_mrt(l,k)>=0;
end
end
cvx_end
% bisection
if strfind(cvx_status,'Solved') % feasible
fprintf(1,'Problem is feasible ',tnext);
wmin = wnext;
else % not feasible
fprintf(1,'Problem not feasible ',tnext);
wmax = wnext;
end
endSome elements of s_k are norm of something (if those assignments don’t trigger error messages, then the something must be affine, but I haven’t spent the time to verify that). So s_k is convex, but not affine.
So norm(s_k...) is a norm of a norm, which is not allowed by CVX. Have you verified that it is convex? if so, a reformulation would be needed.
Thank you very much for reading my trivial code and reply; I think this feasible problem is convex because it has been proved to be a SOCP. I have learned theCVXuserGuide for a whole day, only to find that CVX rejects my model because of the DCP problem. To be honest, this code is my rewritten one, because the first one has some mistakes. you say that norm of a norm is not allowed by cvx, I see.
but the optimal problem that I need to solve is can’t avoid using norm of a norm…which makes me upset.
from the picture, the former element of sk is affine, however, the middle elements of sk are norm; in the last, the element is a scalar. I can not avoid calculating the norm of s_k, (sk),(constraint (39b)) so how to solve this problem? maybe I should use some slack variables to simplify my question. Thanks a lot!
Have you looked carefully at the supposed SOCP formulation? if it really is an SOCP, that should be implementable in CVX.
An SOCP formulation would not have norm of a norm. Any argument of norm would be affine.
Please carefully read the link from my previous post.
But if a,b are vectors then norm([a norm(b)]) = norm([a b]) if I got my sums of squares right… So you can avoid the internal norms.
Thanks for all your reply!
The problem has been solved by introducing some slack variables.
Luckly, it is actually a SOCP.
When I introduce some slack variables, I successfully avoid the question that " norm of a norm"
the final code is below.
cvx_quiet false
while (wmax - wmin >espi||str == 0)
str = 1;
wnext = (wmax+wmin)/2;
cvx_begin sdp
variables XCl(K,1) XWl(Wl,K) YCl(Cl,1) YWl(Wl,1) Z(K,K)
minimize(0)
subject to
for k = 1:K
norm([sqrt(wnext)*[Z((1:(k-1)),k);Z(((k+1):K),k)].*[PhiPhi((1:(k-1)),k);PhiPhi(((k+1):K),k)]; sqrt(wnext)*((BETTAAN((1:Cl),k)-GAMMAAN((1:Cl),k)).^(1/2).*YCl); sqrt(wnext)*(((BETTAAN(Cl+1:L,k)).^(1/2)).*YWl);sqrt(wnext) ])<=XCl(k)+XWl(:,k)'*sqrt(M*GAMMAAN(Cl+1:L,k));
end
for l = 1:Cl
norm(((miu(l,:)).^(1/2))*XCl)<=YCl(l);
YCl(l)<=sqrt(Pd);
end
for l = Cl+1:L
norm(XWl(l-Cl,:))<=YWl(l-Cl);
YWl(l-Cl)<=sqrt(Pd);
end
for k = 1:K
for ii = 1:K
sum(XWl(:,ii).*((M*GAMMAAN(Cl+1:L,k)).^(1.2)))<=Z(ii,k);
end
end
for k = 1:K
XCl(k)>=0;
end
for l = 1:Wl
for k = 1:K
XWl(l,k) >=0;
end
end
cvx_end
% bisection
if strfind(cvx_status,'Solved') % feasible
fprintf(1,'Problem is feasible ',wnext);
wmin = wnext;
else % not feasible
fprintf(1,'Problem not feasible ',wnext);
wmax = wnext;
str = 0;
end
end