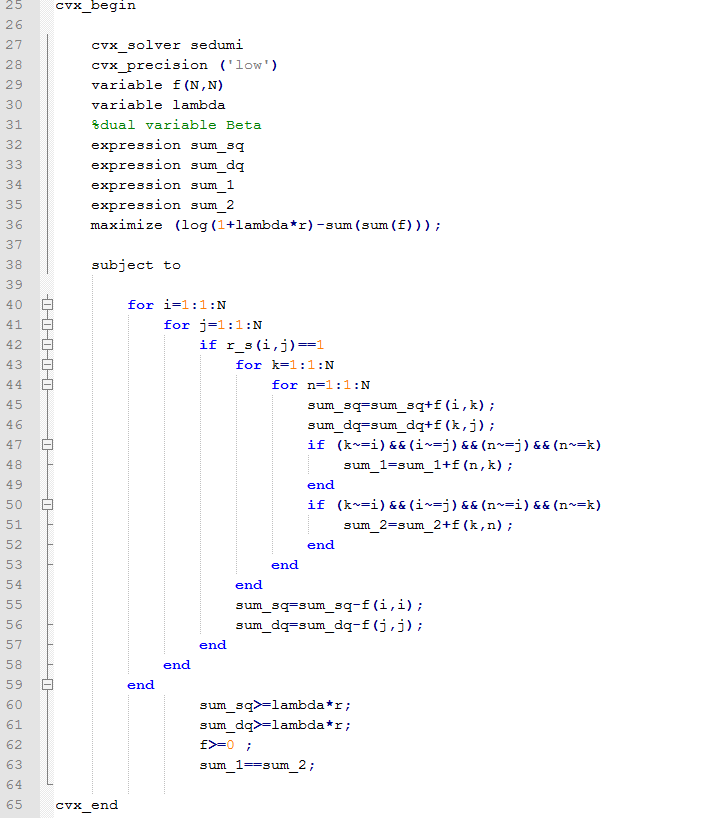
When cvx_precision is set with ‘medium’ and SeDuMi is used , my problem can be solved .While cvx_precision is set with ‘default’ or ‘high’,the status is ‘Inaccurte/Solved’ or ‘Failed’. Besides,when SDPT3 is used, the status is ‘Failed’ no matter what cvx_precision is.
I want to figure out whether it is normal to obtain results like these.
Thank you.
Perhaps you have a difficult, ill-conditioned problem. Does your problem contain coefficients (numbers) of widely varying magnitudes?
Thank you for answering me.
I am new to convex opitimization and CVX,so I don’t know much about it.The opitimization problem is a part of a whole problem in a paper.I don’t know if there is any coefficients of widely varying magnitudes, and I am not sure whether my program is correct.I will continue studying the problem.
By the way ,I hava another question. Quadratic forms are discouraged in CVX,then what I could ues to replace ’ x.*y ',in which x and y are matrice variables.
Well, you must have some problem which you input to CVX, even if it came from a paper. Look at the problem you entered.
x.*y , whether x and y are scalars or matrices, is an indefinite form, and will not be accepted by CVX.
You can enter quadratic forms, such as x’ * A * x, into CVX, where x is a CVX variable (vector) and A is symmetric positive semi-definite. See http://web.cvxr.com/cvx/doc/dcp.html#scalar-quadratic-forms .
Your objective function involves log, so CVX uses its successive approximation method, so you should have received a warning message from CVX. Please read Advanced topics — CVX Users' Guide .
Note the following (from that section)
Second, try different solvers. For instance, SeDuMi and MOSEK tend to be more effective with the successive approximation method than SDPT3. So if the default solver choice fails to give a solution to your model, try switching to one of these solvers.
So numerical problems should not necessarily come as a shock to you. Maybe you can content yourself with SedDuMi in medium precision on this problem. Your best chance at accurately solving a particular problem which requires CVX’s successive approximation method may be if you can use MOSEK as the solver (requires CVX Professional plus MOSEK).
There is a formula like what’s shown below .
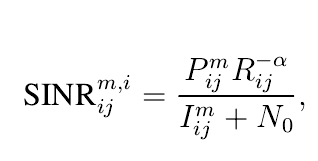
P is variable in my problem,and I is a function for P,which is like this:
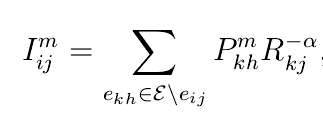
How could I input the first formula to CVX.I have tried to ues ./ and / ,which were not accepted by CVX because of DCP errors.
I’m not sure exactly what your expression is, but note that a/(a+b) is not convex as a function of a and b. So your expression doesn’t look convex to me. If it is convex, prove it.
I can simplify the problem like what’s shown below.
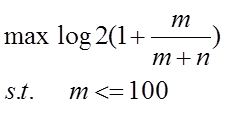
m is a variable and n is constant.The problem is not convex.Then the following inequality is uesd to approximate the function.
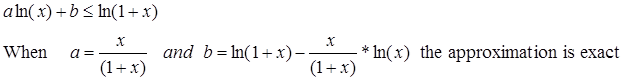
The objective function can be converted into
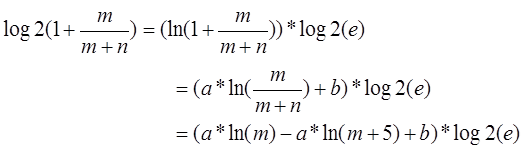
Then define 
,and the problem becomes a convex optimization problem in which a and b
can be estimated 
where x=m/(m+n).
My question is that whether the problem can be accepted and solved by CVX after the transformation.
I have tried as following but there is an error.
Your equality constraint for b is a nonlinear equality constraint, which is non-convex and not accepted by CVX. Your equality constraints for x and a would both be nonlinear equality constraints and therefore not accepted by CVX, except that you forgot the parentheses after the / , and therefore, you have specified x == 6 and a == 2*x, which are linear, convex constraints, although obviously not what you wanted.
Thank you for always answering my questions.
I really forgot the parentheses after the /.So does this mean that the problem can not be solved by CVX? I really can’t find a way to describe the problem in CVX and make it satisfy DCP rules.
I’m still not quite sure exactly what you’re trying to do, or what approximations you are willing to introduce, but your above formulation is non-convex and can not be accepted by CVX.