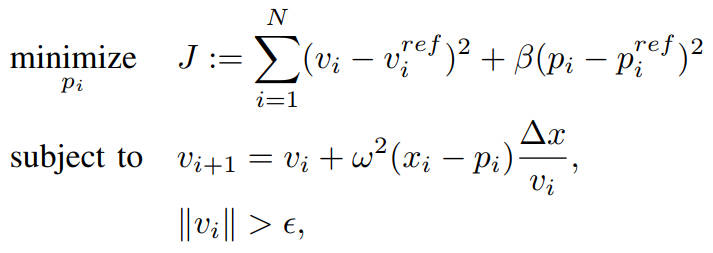I got some DCP problems when using CVX for optimization in Matlab. The object function and some constraints is shown as:
where N is the length of the data array, v^{ref}_i and p^{ref}_i are predifined numbers. I want to optimize the object function to find the optimal v_i and p_i with constant parameters \beta, \omega, \Delta x and \epsinon.
My full code is:
clc; clear; close all;
%% initialization
N = 1500; % data length
x = linspace(0, 1.5, N)’;
delta_x = x(2) - x(1);
% initialize v_ref
v_ref=zeros(N, 1);
v_max = 0.5;
v_max_index_1 = N0.17;
v_max_index_2 = N0.83;
for i=1:1:N
if i < v_max_index_1
v_ref(i) = i*v_max/v_max_index_1;
elseif i > v_max_index_2
v_ref(i) = v_max - (i-v_max_index_2)*v_max/(N-v_max_index_2);
else
v_ref(i) = v_max;
end
end
% initialize p_ref
p_ref=zeros(N, 1);
step_pos = [0, 0.5, 1.0, 1.5]’;
step_pos_index = [[0.13N, 0.2N]; [0.47N, 0.53N]; [0.8N, 0.87N]];
% temporary variables for p_ref initialization
step_pos_tmp = [step_pos; step_pos(end)];
step_pos_index_tmp = [step_pos_index; [N, N]];
step_num = 1;
for i=1:1:N
if i < step_pos_index_tmp(step_num, 1)
p_ref(i) = step_pos_tmp(step_num);
elseif i >= step_pos_index_tmp(step_num, 2)
p_ref(i) = step_pos_tmp(step_num+1);
step_num = step_num + 1;
else
p_ref(i) = step_pos_tmp(step_num) + (i-step_pos_index_tmp(step_num,1))*(step_pos_tmp(step_num+1) - step_pos_tmp(step_num))/(step_pos_index_tmp(step_num,2) - step_pos_index_tmp(step_num,1));
end
end
% optimization
beta = 1;
z = 1.0;
g = 9.81;
omega = sqrt(g/z);
epsinon = 0.005;
v = zeros(N, 1);
p = zeros(N, 1);
v(1) = 1e-6;
cvx_begin quiet
variables v(N) p(N)
minimize(sum_square_abs(v - v_ref) + sum_square_abs(p - p_ref))
subject to
for i=1:N-1
v(i+1) == v(i) + pow_pos(omega, 2)*(x(i) - p(i))*delta_x/v(i);
% norm(v(i), 2) >= epsinon;
end
cvx_end
cvx_status
cvx_optval
%% plot
figure(1);
line_width = 1.5;
subplot(2,1,1);
plot(x, p_ref, ‘r–’, ‘linewidth’, line_width);
hold on;
plot(x, p, ‘b’, ‘linewidth’, line_width);
hold off;
legend({‘ZMPref’, ‘ZMP’}, ‘Location’, ‘northwest’);
ylim([-0.1, 1.7]);
xlabel(‘x[m]’);
ylabel(‘ZMP[m]’);
subplot(2,1,2);
plot(x, v_ref, ‘r–’, ‘linewidth’, line_width);
hold on;
plot(x, v, ‘b’, ‘linewidth’, line_width);
hold off;
legend({‘Vref’, ‘V’}, ‘Location’, ‘northwest’);
ylim([0, 0.9]);
xlabel(‘x[m]’);
ylabel(‘v[m/s]’);
My problem is the expression “v(i+1) == v(i) + pow_pos(omega, 2)*(x(i) - p(i))*delta_x/v(i);” violates the DCP rules, and I found that the last item of the expression “/(vi)” caused the problem, the errors from Matlab is:
错误使用 .* (line 173)
Disciplined convex programming error:
Cannot perform the operation: {real affine} ./ {real affine}
出错 ./ (line 19)
z = times( x, y, ‘./’ );
出错 * (line 36)
z = feval( oper, x, y );
出错 / (line 15)
z = mtimes( x, y, ‘rdivide’ );
出错 demo_SQD (line 67)
v(i+1) == v(i) + pow_pos(omega, 2)*(x(i) - p(i))*delta_x/v(i);
Dose anyone know how to make it works? Thanks for your help.